






Федеральное агентство по образованию
Государственное образовательное учреждение высшего
профессионального образования
Тульский государственный университет
Кафедра прикладной математики и информатики
Математическое моделирование
Лабораторная работа №4
“ Исследование распространения упругих волн
в анизотропной пластине.”
Выполнил студент группы
Принял
Исследование распространения упругих волн в анизотропной пластине.
ТЕОРЕТИЧЕСКАЯ СПРАВКА:
Закон Гука для плоского деформированного состояния в анизотропной среде имеет вид
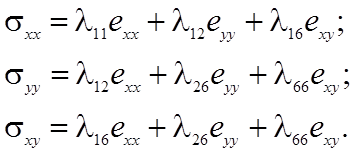 (1)
(1)
Здесь 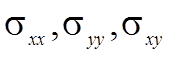 – компоненты тензора
напряжения,
– компоненты тензора
напряжения, 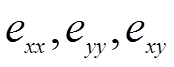 – компоненты тензора деформации или
относительное удлинение относительно координатной оси
– компоненты тензора деформации или
относительное удлинение относительно координатной оси
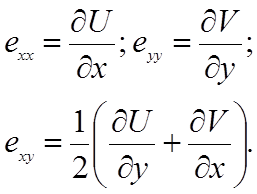 (2)
(2)
Уравнения движения материальных точек среды твердого тела в напряжениях запишутся так:
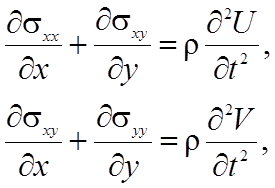 (3)
(3)
где r – плотность материала; (U, V) – проекции вектора перемещения на оси х, у.
Подставим соотношения (2) в уравнения (1):
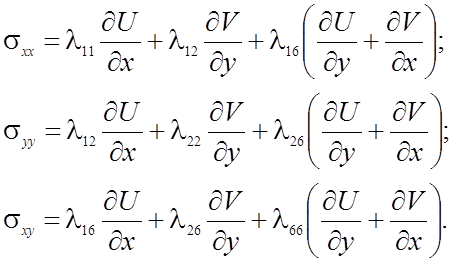 (4)
(4)
Подставив формулы (4) в уравнения (3), получим уравнение движения в перемещениях:
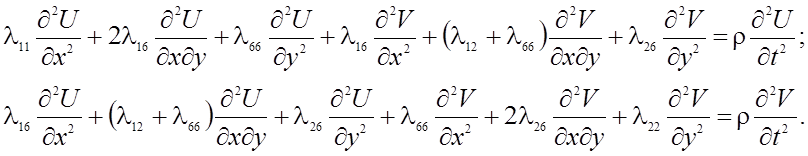 (5)
(5)
Пусть в плоскости (х, у) распространяется плоская волна вида
![]() (6)
(6)
Следовательно,
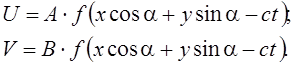 (7)
(7)
Подставим (7) в уравнение (5):
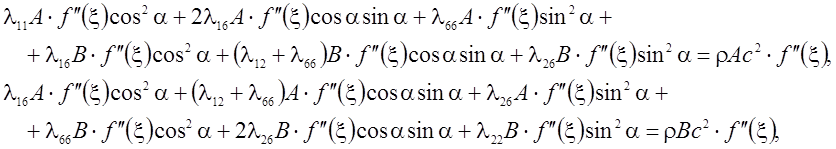
где ![]() .
.
Получим
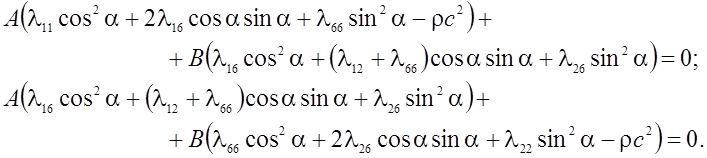
Полученную систему представим в виде
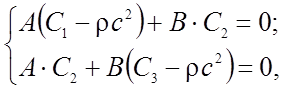 (6)
(6)
где
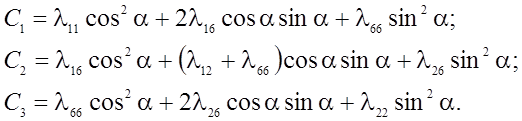 (7)
(7)
Так как в общем случае А и В одновременно не равны нулю, то определитель системы (6) должен быть равен нулю
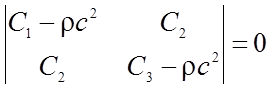 ,
,
![]()
![]() , и для с получим уравнение
, и для с получим уравнение
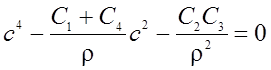 .
(8)
.
(8)
Решая это уравнение, получим
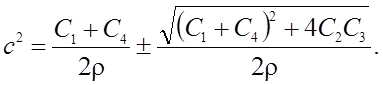 (9)
(9)
Из выражения (9) для квадрата скорости плоской волны (для каждой координатной плоскости), распространяющейся в анизотропной среде, можно заключить, что в безграничной трехмерной среде для каждого направления существуют три действительных скорости распространения волны и скорости этих волн зависят от направления распространения волны.
Как известно, для
упругой изотропной среды для каждого направления существуют лишь две действительные
скорости распространения волн ![]() и
и ![]() , и они не зависят от направления
распространения волн.
, и они не зависят от направления
распространения волн.
ИССЛЕДОВАНИЕ ЗАДАЧИ С ПОМОЩЬЮ ПАКЕТА MAPLE:
restart;
rho:=7.7;
![]()
E1:=3e5;
![]()
E2:=3.4e5;
![]()
G2:=0.21e5;
![]()
nu12:=0.134;
![]()
nu21:=0.15;
![]()
lambda11:=E1/(1+nu12*nu21);
lambda12:=nu21*E1/(1+nu12*nu21);
lambda16:=1.44e5;
lambda22:=E2/(1+nu12*nu21);
lambda26:=0.71e5;
lambda66:=G2;
![]()
![]()
![]()
![]()
![]()
![]()
C1:=(alpha)->lambda11*(cos(alpha))^2+2*lambda16*cos(alpha) *sin(alpha)+lambda66*(sin(alpha))^2;
C2:=(alpha)->lambda16*(cos(alpha))^2+(lambda16+lambda66)*cos(alpha) *sin(alpha)+lambda26*(sin(alpha))^2;
C3:=(alpha)->lambda66*(cos(alpha))^2+2*lambda26*cos(alpha)
*sin(alpha)+lambda22*(sin(alpha));
![]()
![]()
![]()
c1:=(alpha)->(C1(alpha)+C2(alpha))/2/rho+sqrt((C1(alpha)*C1(alpha)-C3(alpha)*C3(alpha))^2+4*C2(alpha)*C2(alpha))/2/rho;
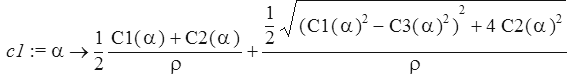
c2:=(alpha)->(C1(alpha)+C2(alpha))/2/rho-sqrt((C1(alpha)*C1(alpha)-C3(alpha)*C3(alpha))^2+4*C2(alpha)*C2(alpha))/2/rho;
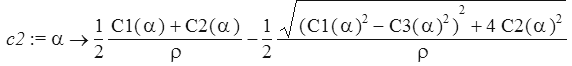
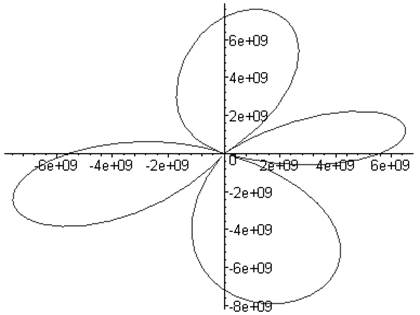
plot(c1(alpha),alpha=0..6.28,coords=polar);
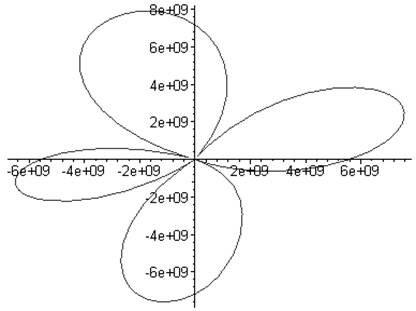
plot(c2(alpha),alpha=0..6.28,coords=polar);
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.