Федеральное агентство по образованию
Государственное образовательное учреждение высшего
профессионального образования
Тульский государственный университет
Кафедра прикладной математики и информатики
Математическое моделирование
Лабораторная работа №1
“Моделирование задачи теплового удара
на поверхности полупространства”
Выполнил студент группы
Принял
Приобретение навыков моделирования задачи теплового удара на поверхности полупространства.
ТЕОРЕТИЧЕСКАЯ СПРАВКА:
Рассмотрим полупространство, занимающее область ![]() при
тепловом ударе га его поверхности
при
тепловом ударе га его поверхности ![]() . Пусть начальная
температура полупространства и среды, омывающей его поверхность
. Пусть начальная
температура полупространства и среды, омывающей его поверхность ![]() , равна
, равна ![]() . В
момент
. В
момент ![]() полупространство подвергалось тепловому воздействию
среды, температура которой мгновенно повышается до значения
полупространство подвергалось тепловому воздействию
среды, температура которой мгновенно повышается до значения ![]() .
.
Между
средой и поверхностью в дальнейшем происходит конвективный теплоомен.
Нестационарное температурное поле полупространства ![]() при
отсутствии источников тепла описывается уравнением
при
отсутствии источников тепла описывается уравнением
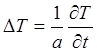 , (1)
, (1)
где ![]() - температуропроводность материала
полупространства, и условиями
- температуропроводность материала
полупространства, и условиями
![]() при
при ![]() (2)
(2)
(распределение температуры в начальный момент времени)
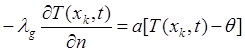 (3)
(3)
(граничное условие), где ![]() - коэффициент теплопроводности,
- коэффициент теплопроводности, ![]() - коэффициент теплоотдачи на
поверхности,
- коэффициент теплоотдачи на
поверхности, ![]() - внешняя нормаль к поверхности.
- внешняя нормаль к поверхности.
Для рассматриваемой одномерной задачи выражения (1)-(3) принимают вид
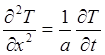 ; (4)
; (4)
![]() при
при ![]() ; (5)
; (5)
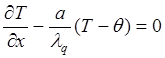 при
при ![]() (6)
(6)
В граничном
условии (6) учитывается, что направление внешней нормали к поверхности ![]() противоположно направлению оси
противоположно направлению оси ![]() .
.
Применим
интегральное преобразование Лапласа к уравнению (4) и условиям (5) и (6). Имеем
![]() . Отсюда
. Отсюда
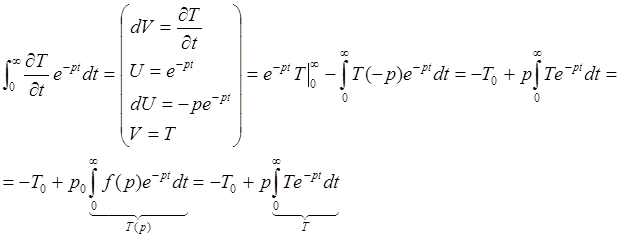
![]()
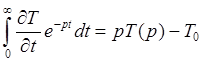 ;
;
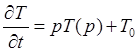
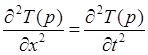
![]()
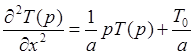
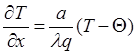 при х=0
при х=0 ![]()
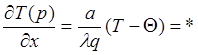
С учетом 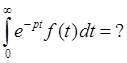
![]()
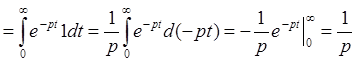
![]()
Тогда ![]()
![]()
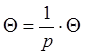
* =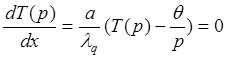 (8)
(8)
Решение уравнения (4) в частных производных сводится к решению обыкновенного дифференциального уравнения
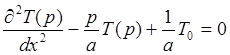 (7)
(7)
![]()
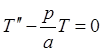
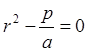
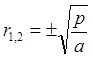
Общее решение: ![]()
Частное решение: ![]()
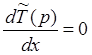
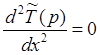
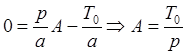
![]()
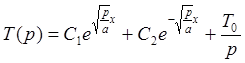 (9)
(9)
Здесь
следует положить ![]() , так как температура с
увеличением
, так как температура с
увеличением ![]() не должна возрастать. Поэтому
не должна возрастать. Поэтому
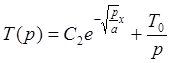 (10)
(10)
Подставляя (10) в уравнение (8), находим
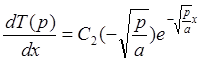
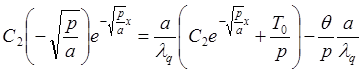
х=0, поэтому 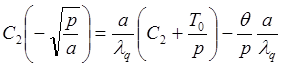
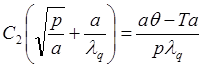
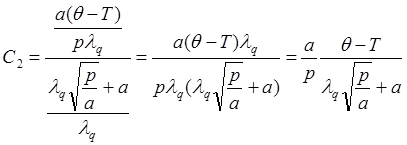 (11)
(11)
Следовательно, изображение температуры полупространства
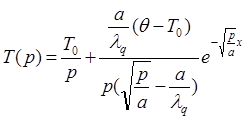 (12)
(12)
Изпользуя для нахождения оригинала таблицу, находим искомое решение:
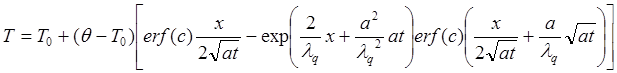 (13)
(13)
где ![]() ;
; 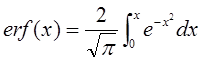 -
интеграл вероятности.
-
интеграл вероятности.
МАШИННАЯ РЕАЛИЗАЦИЯ алгоритма:
> restart;
> T:=(T0,Q,a,alpha,lambda,t,x)->T0+(Q-T0)*(erfc(x/(2*sqrt(a*t)))-exp(2*x/lambda+alpha^2/lambda^2*a*t)*erfc(x/(2*sqrt(a*t))+alpha/lambda*sqrt(a*t)));
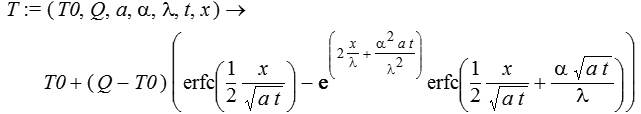
> Q:=100*13;T0:=50;
![]()
![]()
> alpha:=3;lambda:=0.5;a:=0.5;
![]()
![]()
![]()
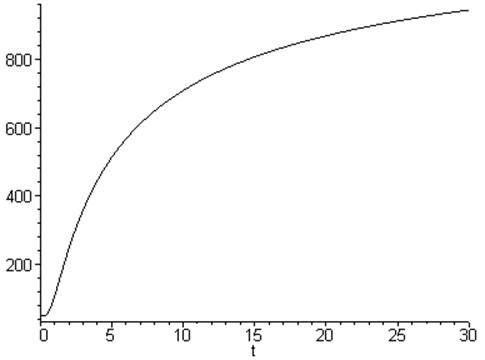
> plot(T(T0,Q,a,alpha,lambda,t,2),t=0..30)
|
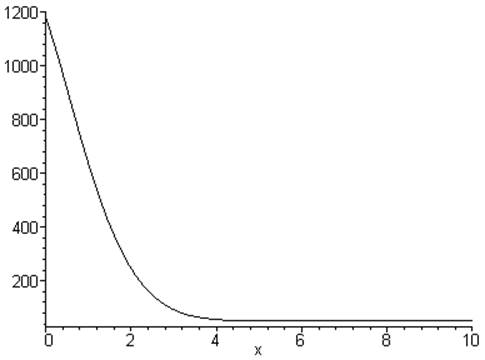
> plot(T(T0,Q,a,alpha,lambda,2,x),x=0..10);
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.