



Теория вероятностей и мат. стат.
1. Квантиль порядка р — это
1) значение случайной величины, вероятность которой равна р
2) значение случайной величины, вероятность отклонения которого от математического ожидания равна р
3) значение случайной величины, при котором функция плотности распределения равна р
4) значение случайной величины, при котором функция распределения равна р 2. Второй центральный момент случайной величины связан со вторым начальным моментом соотношением
1) больше
2) меньше
3) не больше
4) не меньше
3. Коэффициент вариации случайной величины выражает
1) близость закона распределения случайной величины к нормальному
2) относительную изменчивость случайной величины
3) степеньнесимметричностираспределения случайной величины
4) степеньостровершинностизаконараспределения случайной величины
4. Из приемного бункера детали для обработкизабираютсячерезкаждые 10 минут. Какова дисперсия времени ожидания детали в бункере?
1) 5,0
2) 8,3
3) 10,0
4) 25,0
5. Из приемного бункера детали для обработкизабираютсячерезкаждые 18 минут. Какова дисперсия времени ожидания детали в бункере?
1) 9
2) 18
3) 27
4) 36
6. ВремяобработкизаявкинаЭВМподчиняется показательному распределению со средним значением 3 мин. Чему равен коэффициент ва риации времени обработки заявки на ЭВМ?
1) 0,3
2) 0,53) 1
4) 1,5
7. Правило ”трехсигм” длянормальногозакона гласит:
1) с точностью до тысячных диапазон разброса значений случайной величины заключен впределахплюс-минустриСКОотматематического ожидания
2) с точностью до тысячных коэффициент вариации случайной величины не превышает значения трех СКО
3) с точностью до тысячных разность между максимальным и минимальным значением случайной величины не превышает трех СКО
4) три значения СКО определяют степень приближения закона случайной величины к нормальному
8. Функция распределения расхода материала
(кг) и полученной прибыли (руб.) имеет размерность
1)
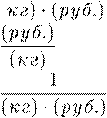 (
(
2)
3)
4) безразмерна
9. Функция плотности распределения затрат сырья (кг) и себестоимости единицы продукции (руб.) имеет размерность
1)
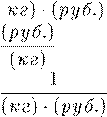 (
(
2)
3)
4) безразмерна
10. Ковариационный момент связи диаметра втулки (см) исебестоимостьюееизготовления (руб.) имеет размерность
1)
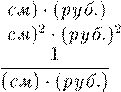 (
(
2) (
3)
4) безразмерен
11. Условный закон распределения величины
Х — это
1) закон распределения величины Х при условии, что величина Y не влияет на Х
2) закон распределения величины Х при условии, что величина Y не коррелирована с Х
3) закон распределения величины Х при условии, что величина Y приняла определенное значение
4) закон распределения величины Х при условии, что величина Х не зависит от Y 12. Если случайные величины Х и Y умножить соответственно на 2 и 3 и прибавить к каждой значение 4, то коэффициент корреляции
1) не изменится √
2)
увеличится в 6![]() раз
раз
3) увеличится в 4 раза
4) увеличится в 6 раз
13. Композиция двух одинаковых равномерно распределенныхслучайнойвеличиныдаетраспределение
1) нормальное
2) показательное
3) равномерное
4) треугольное
14. Композиция двух законов Пуассона дает распределение
1) биномиальное
2) гипергеометрическое
3) нормальное
4) Пуассона
15. Одинстанокдаетвсреднем 3% брака, другой — 5%. Производительностистанководинаковы. Каковкоэффициентвариациичислабракованных изделий в общей продукции из 100 деталей?
1) 0,3
2) 0,4
3) 0,5
4) 0,8
16. Закон распределения называется устойчивым, если
1) при композиции двух законов этого типа вновь получается закон этого же типа
2) при композиции двух законов этого типа дисперсия суммы двух случайных величин не больше суммы дисперсий
3) при увеличении числа данных коэффициент вариации уменьшается
4) при увеличении числа наблюдений диспе рсия случайной величины уменьшается
17. Все формы закона больших чисел устанавливают
1) доверительныеграницыдляосновныхчисловых параметров распределения случайных величин
2) предельные значения параметров закона распределения случайных величин
3) условия, при которых возникает нормальный закон распределения
4) факт сходимости по вероятности тех или иных случайных величин к определенным постоянным
18. Характеристическая функция случайной величины Х — это
1) математическое ожидание величины eitx, рассматриваемое как комплексная функция действительной переменной t
2) преобразованиеФурьевеличиныХ дляперехода в комплексную область ее значений
3) функция взаимосвязи центральных и начальных моментов случайной величины Х
4) функция, обеспечивающая вычисление основных характеристических законов распределения случайной величины Х по ее центральным моментам
19. Полигон распределения случайной величины Х — это
1) вариационный ряд случайной величины Х, представленный в виде столбчатой диаграммы
2) графическое представление дискретного статистического распределения случайной величины Х
3) размах значений случайной величины Х
4) ступенчатая фигура изменения значений случайной величины Х нарастающим итогом
20. Выборка называется репрезентативной, если
1) она организована повторным и бесповторным отбором элементов из генеральной совокупности
2) она организована случайно из элементов генеральной совокупности
3) она отражает основные характеристики генеральной совокупности
4) она отражает структуру генеральной совокупности
21. Оценка называется несмещенной, если
1) математическое ожидание оценки равно искомому параметру
2) она вычислена по всей имеющейся статистической совокупности
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.