


























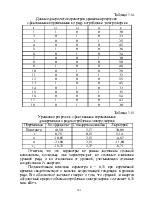









Ряды динамики подразделяют на ряды динамики абсолютных, средних и относительных величин.
По признаку времени ряды динамики абсолютных величин подразделяют на моментные и интервальные ряды динамики.
Моментный ряд динамики – это ряд, который образуют показатели, характеризующие состояние явления на тот или иной момент времени.
Интервальный ряд динамики – ряд, который образуют показатели, характеризующие явление за тот или иной период времени.
Для общей характеристики уровня явления за тот или иной период вычисляется средняя из всех уровней ряда – средний уровень ряда.
Способ расчета среднего уровня ряда зависит от характера ряда.
Средний уровень ряда часто определяют по формуле
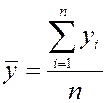 , где
n – число
членов ряда динамики.
, где
n – число
членов ряда динамики.
Абсолютный прирост ![]() показывает, на
сколько единиц увеличился (или уменьшился) анализируемый уровень ряда
показывает, на
сколько единиц увеличился (или уменьшился) анализируемый уровень ряда ![]() относительно базисного уровня
относительно базисного уровня ![]() (по базисной схеме) или уровня
предшествующего года
(по базисной схеме) или уровня
предшествующего года ![]() (по цепной схеме).
(по цепной схеме).
Абсолютный прирост определяют по формулам:
![]() (по базисной
схеме),
(по базисной
схеме),
![]() (по цепной
схеме).
(по цепной
схеме).
Темп роста ![]() показывает, во сколько раз
анализируемый уровень ряда увеличился по сравнению с уровнем, принятым за базу
сравнения (по базисной схеме) или предшествующим уровнем (по цепной схеме), или
какую долю анализируемый уровень ряда составляет от уровня ряда, принятого за
базу сравнения. Темп роста выражают в процентах или отвлеченных числах
(коэффициент роста).
показывает, во сколько раз
анализируемый уровень ряда увеличился по сравнению с уровнем, принятым за базу
сравнения (по базисной схеме) или предшествующим уровнем (по цепной схеме), или
какую долю анализируемый уровень ряда составляет от уровня ряда, принятого за
базу сравнения. Темп роста выражают в процентах или отвлеченных числах
(коэффициент роста).
Темп роста определяют по формулам:
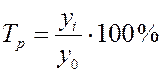 (по базисной схеме),
(по базисной схеме),
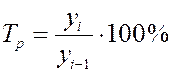 (по цепной схеме).
(по цепной схеме).
Темп прироста ![]() показывает, на
сколько процентов увеличился (или уменьшился) анализируемый уровень ряда по
сравнению с базисным (по базисной схеме), или предшествующим уровнем ряда (по
цепной схеме).
показывает, на
сколько процентов увеличился (или уменьшился) анализируемый уровень ряда по
сравнению с базисным (по базисной схеме), или предшествующим уровнем ряда (по
цепной схеме).
Темп прироста определяют как отношение абсолютного прироста к уровню, принятому за базу сравнения по формулам:
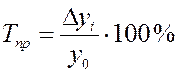 (по базисной
схеме).
(по базисной
схеме).
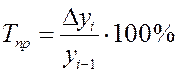 (по цепной
схеме).
(по цепной
схеме).
Темпы роста и прироста связаны между собой, что видно из формул их расчета
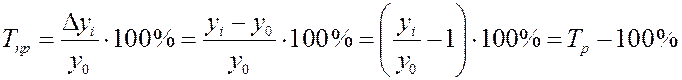 .
.
Это дает основание определить темп прироста через темп роста:
![]() .
.
Средний темп роста и средний темп прироста характеризуют соответственно темпы роста и прироста за период в целом.
Средний темп роста рассчитывается по данным ряда динамики по формуле средней геометрической:
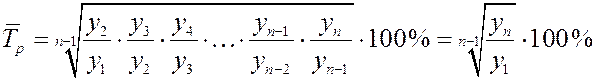 , где
n–1
– количество цепных коэффициентов роста.
, где
n–1
– количество цепных коэффициентов роста.
Средний темп прироста можно определить из среднего темпа роста:
![]() .
.
Абсолютное значение одного процента прироста –
это отношение абсолютного прироста к цепному темпу прироста, выраженному в процентах:
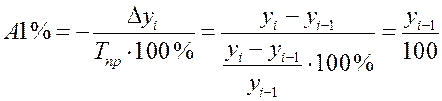 .
.
Абсолютное значение одного процента прироста равно 0.01 предшествующего уровня.
Для сравнения базисных темпов роста двух изучаемых рядов динамики за
анализируемый период принято исчислять коэффициент опережения ![]() по формуле
по формуле
![]() , где
, где
![]() – базисный темп роста первого ряда;
– базисный темп роста первого ряда;
![]() – базисный темп роста второго ряда.
– базисный темп роста второго ряда.
Уровни рядов динамики должны быть сопоставимы по методологии рассчёта показателя, территории, продолжительности периодов, охватываемого объекта, единицам измерения и другим признакам.
В тех случаях, когда вначале имеются уровни ряда, исчисляемые по одной методологии или в одних границах, а затем уровни ряда, исчисляемые по другой методологии или в других границах, уровни ряда динамики оказываются несопоставимы между собой. Чтобы привести уровни в ряду динамики к сопоставимому, годному для анализа виду, необходимо применить приём, который называют смыканием рядов динамики [26, 55].
Пример 7.1. Имеются данные о поголовье скота в районе (табл.7.1).
Привести ряды динамики к сопоставимому виду.
Таблица 7.1.
Динамика поголовья скота в районе за 1996 - 2002 гг. (тыс. голов)
|
№ п\п |
Поголовье крупного рогатого скота |
Год |
||||||
|
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
2002 |
||
|
1 |
В прежних границах |
45,0 |
48,0 |
50,0 |
- |
- |
- |
- |
|
2 |
В новых границах |
- |
- |
70,0 |
71,3 |
73,2 |
74,1 |
75,0 |
|
3 |
Сомкнутый ряд |
63,0 |
67,2 |
70,0 |
71,3 |
73,2 |
74,1 |
75,0 |
Решение. Определим коэффициент пересчёта уровней в 1998 г., в котором произошло
изменение границ района: ![]() .
.
Умножая на этот коэффициент уровни ряда динамики в прежних границах, приводим их к сопоставимым уровням в новых границах.
В 1996 г.: ![]() тыс. голов; в 1997г.:
тыс. голов; в 1997г.: ![]() тыс. голов.
тыс. голов.
Представим полученные данные в виде сомкнутого ряда динамики (третья строчка табл. 7.1).
Эти данные сопоставимого ряда характеризуют рост поголовья скота в районе за 1996 - 2002 гг. Они могут быть использованы для расчёта аналитических показателей ряда динамики.
Пример 7.2. Имеются данные о среднемесячной заработной плате на одного работника и стоимости набора из 25 основных продуктов питания в расчёте на одного человека в одной из областей РФ за полугодие:
|
Месяц |
Среднемесячная заработная плата, руб. |
Стоимость набора из 25 основных продуктов питания, руб. |
|
Январь |
6548 |
2094 |
|
Февраль |
6844 |
2166 |
|
Март |
7450 |
2209 |
|
Апрель |
7465 |
2241 |
|
Май |
7793 |
2275 |
|
Июнь |
8372 |
2325 |
Привести ряды динамики к одному основанию и сделать краткие выводы.
Решение. Для сравнения показателей необходимо уровни рядов привести к одному основанию, т.е. исчислить базисные темпы роста.
Для среднемесячной заработной платы:
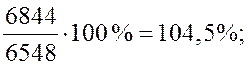
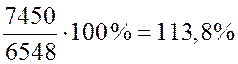 и т.д.
и т.д.
Для стоимости набора продуктов питания:
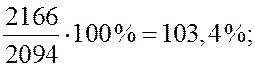
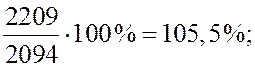 и т.д.
и т.д.
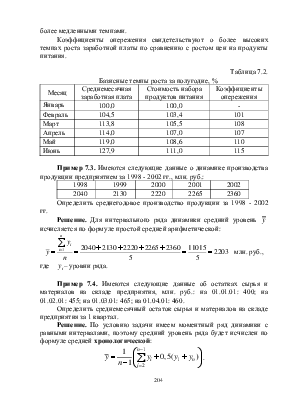
Представим полученные результаты в табл. 7.2.
Данные табл. 7.2 показывают, что начисленная среднемесячная заработная плата на одного работника неуклонно растёт.
Прирост в июне к январю составил 27,9 %. С
тоимость набора из 25 основных продуктов питания тоже растёт, но более
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.