Задача:
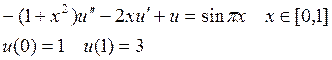
Решить приближенно задачу, применив к ней вариационные методы: метод Ритца и наименьших квадратов.
Если данное уравнение записать в виде:
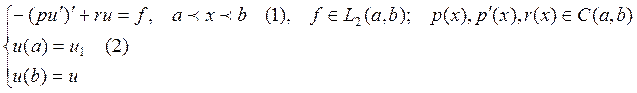
или
![]()
![]()
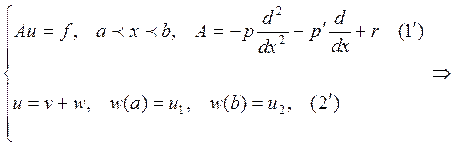
![]()
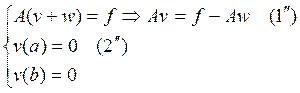
Приближенное решение задачи будем искать в виде:
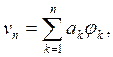 где
где ![]() - n-ое
приближение точного решения
- n-ое
приближение точного решения 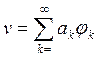 ,
, ![]() - элементы последовательности функций,
которые образуют базис, в так называемом энергетическом пространстве
- элементы последовательности функций,
которые образуют базис, в так называемом энергетическом пространстве ![]() , со скалярным произведением:
, со скалярным произведением:
![]() , а
, а ![]() - образуют числовую последовательность, A –
положительно определенный оператор.
- образуют числовую последовательность, A –
положительно определенный оператор.
I. Решим задачу методом Ритца, используя в качестве базисных функций 2 вида функций.
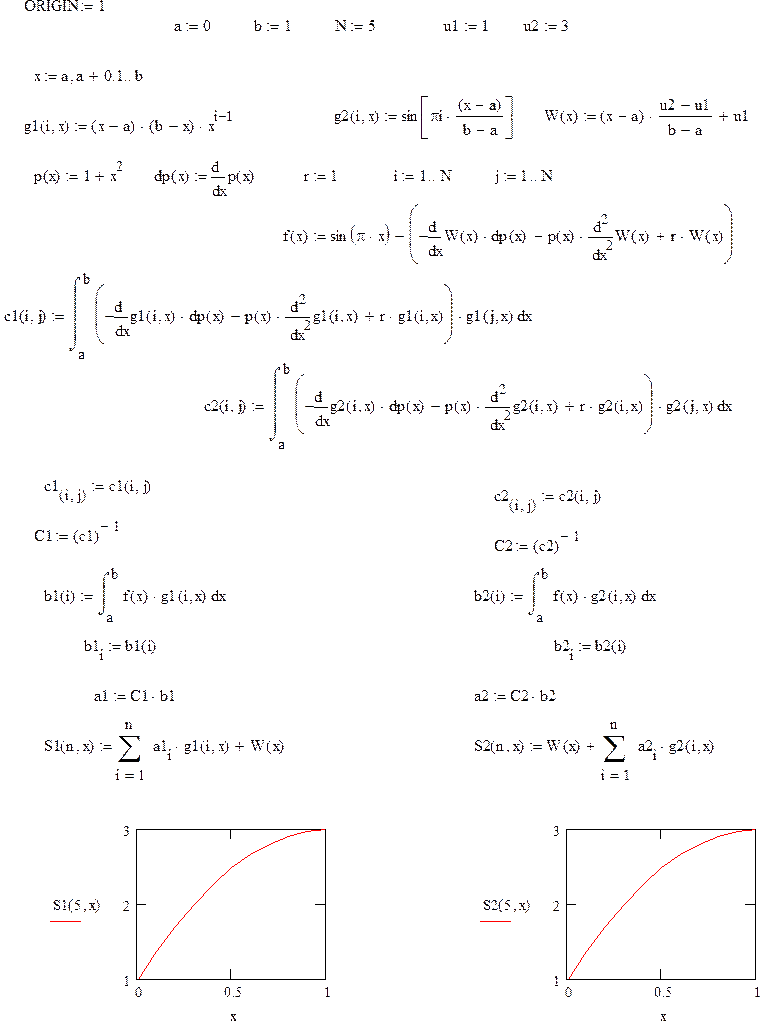
II. Решим задачу методом наименьших квадратов, используя в качестве базисных функций 2 вида функций.
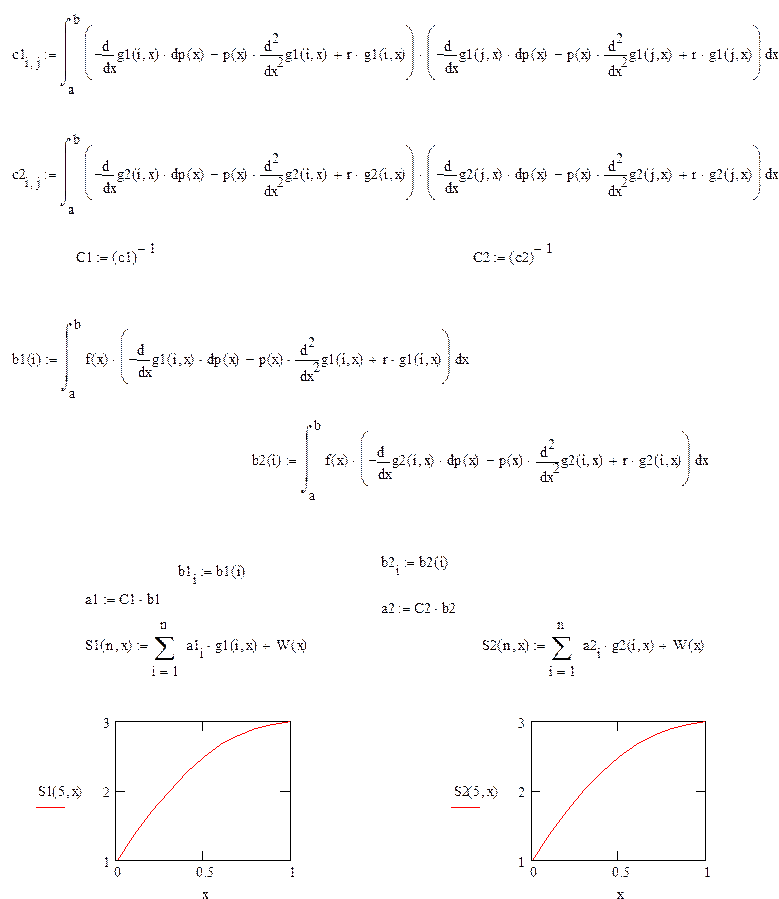
III. Решим задачу методом Ритца, используя контрольный пример, а в качестве базисных функций 2 вида функций.
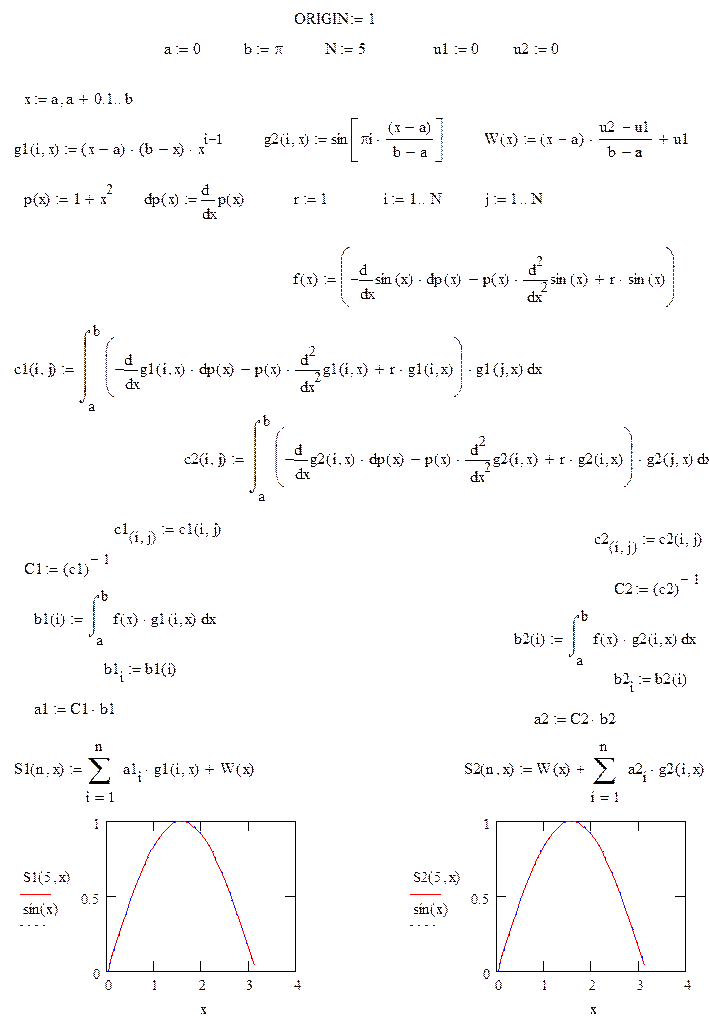
IV. Решим задачу методом наименьших квадратов, используя контрольный пример, а в качестве базисных функций 2 вида функций.
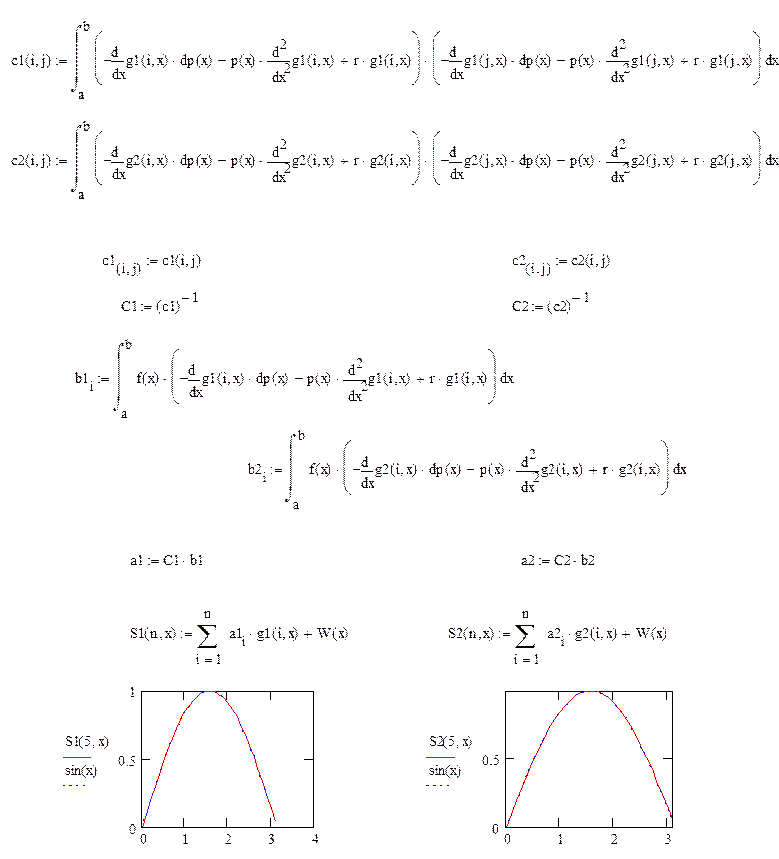
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.