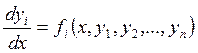 можно интерпретировать
геометрически как кривую в
можно интерпретировать
геометрически как кривую в 3.
Всегда ли методом исключения можно привести нормальную систему ![]() уравнений к одному уравнению
уравнений к одному уравнению ![]() - го порядка с одной неизвестной
функцией? НЕТ
- го порядка с одной неизвестной
функцией? НЕТ
7.
Если известна фундаментальная система решений ![]() однородного уравнения
однородного уравнения ![]() , то общее решение соответствующего
неоднородного уравнения
, то общее решение соответствующего
неоднородного уравнения ![]() может быть
найдено по формуле
может быть
найдено по формуле ![]() , где функция
, где функция ![]() определяется из системы уравнений:
определяется из системы уравнений: 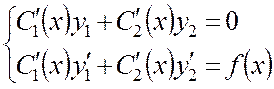
8.
Если число ![]() является корнем
кратности
является корнем
кратности ![]() характеристического уравнения
соответствующего однородного уравнения, то частное решение неоднородного
уравнения имеется в виде:
характеристического уравнения
соответствующего однородного уравнения, то частное решение неоднородного
уравнения имеется в виде: ![]()
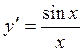 :????????
:????????10. Исследовать на
устойчивость нулевое решение системы 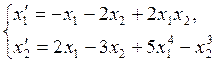 НУЛЕВОЕ
РЕШЕНИЕ СИСТЕМЫ АССИМПТОТИЧЕСКИ УСТОЙЧИВО ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ.
НУЛЕВОЕ
РЕШЕНИЕ СИСТЕМЫ АССИМПТОТИЧЕСКИ УСТОЙЧИВО ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ.
11. Исследовать
устойчивость решения ![]() системы
системы 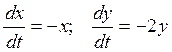 : НУЛЕВОЕ РЕШЕНИЕ СИСТЕМЫ
АССИМПТОТИЧЕСКИ УСТОЙЧИВО.
: НУЛЕВОЕ РЕШЕНИЕ СИСТЕМЫ
АССИМПТОТИЧЕСКИ УСТОЙЧИВО.
12. Исследовать, является
ли решение ![]() устойчивым для системы
устойчивым для системы 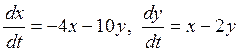 : УСТОЙЧИВО, НО НЕ
АССИМПТОТИЧЕСКИ
: УСТОЙЧИВО, НО НЕ
АССИМПТОТИЧЕСКИ
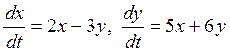 . НЕТ
. НЕТ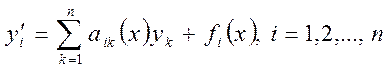
15. Каким методом интегрируется линейное неоднородное уравнение? Методами Бернулли, Лагранжа, неопределенных коэффициентов
16.
Как интегрируется уравнение Бернулли ![]() ?
Любым из указанных методов
(методом Лагранжа, Бернулли, подстановкой
?
Любым из указанных методов
(методом Лагранжа, Бернулли, подстановкой ![]() )
)
17. Как
находится общее решение уравнения Клеро? Введение параметра ![]() или заменой в уравнении
или заменой в уравнении ![]() на
на ![]()
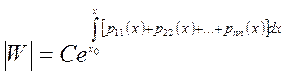
19.
Какое решение называется особым? Решение ![]() , в каждой точке
которого нарушается единственность решения задачи Коши
, в каждой точке
которого нарушается единственность решения задачи Коши
20. Какое уравнение с неизвестной функцией называется обыкновенным дифференциальным уравнением? Уравнение, которое содержит производные от искомой функции и может содержать искомую функцию и независимую переменную
21.
Какой вид имеет неоднородное линейное уравнение ![]() -
го порядка?
-
го порядка? 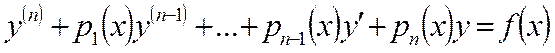
22.
Какой вид имеет уравнение Клеро? 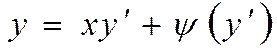
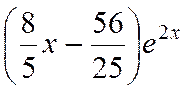
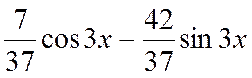
28.
Как при помощи определителя Вронского узнать, образуют ли данные ![]() решений однородного линейного
уравнения
решений однородного линейного
уравнения ![]() - го порядка фундаментальную систему
решений?
- го порядка фундаментальную систему
решений? ![]()
29.
Как строится общее решение однородного линейного уравнения ![]() - го порядка по фундаментальной
системе решений?
- го порядка по фундаментальной
системе решений? 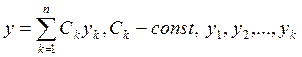 - фундаментальная система решений
уравнения
- фундаментальная система решений
уравнения ![]()
30. Линейная однородная система с постоянными коэффициентами всегда интегрируется в элементарных функциях. Это можно показать, используя метод: метод Эйлера
31.
Линейное дифференциальное уравнение второго порядка имеет вид ![]() . Если корни
. Если корни ![]() и
и
![]() характеристического уравнения
действительны и равны, то общее решение уравнения записывается в виде:
характеристического уравнения
действительны и равны, то общее решение уравнения записывается в виде: ![]()
32.
Линейное дифференциальное уравнение второго порядка имеет вид ![]() . Если корни
. Если корни ![]() и
и
![]() характеристического уравнения
действительны и различны, то общее решение уравнения записывается в виде:
характеристического уравнения
действительны и различны, то общее решение уравнения записывается в виде: 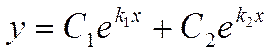
33.
Линейное дифференциальное уравнение второго порядка имеет вид ![]() . Если корни
. Если корни ![]() и
и
![]() характеристического уравнения
комплексные числа, то общее решение уравнения записывается в виде:
характеристического уравнения
комплексные числа, то общее решение уравнения записывается в виде: ![]()
34. Метод
исключения решения нормальных систем уравнений ![]() -
го порядка
-
го порядка
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.