Численные методы. Условие сходимости метода итераций решения нелинейного уравнения. Формула метода Ньютона решения нелинейного уравнения

Численные методы

1.1. Отделениекорнейприрешениинелинейного уравнения — это

A)  установление возможно более тесных промежутков [α,β], в которых содержится только по одному корню.

B)  нахождение приближенных значений корней.

C)  нахождение какого-либо одного корня.

1.2. Методдихотомииприрешениинелинейного уравнения применяется тогда, когда A) требуется высокая надежность счета.

B)  требуется высокая скорость счета.

C)  требуется высокая надежность и высокая скорость счета.

1.3.  Расчетная формула метода итераций для нахождениярешениянелинейногоуравненияимеет вид:

A)

                     xn+1 = ϕ(xn),               n = 1,2,....

B)

                     xn = ϕ(xn+1),               n = 1,2,....

C)

                   xn+1 = ϕ(xn+1),                n = 1,2,....

1.4.  Условие сходимости метода итераций решения нелинейного уравнения, приведенного к виду x = ϕ(x), имеет вид:

A)

|ϕ⁰(x)| < 1

B)

|ϕ⁰(x)| > 1

C)

|ϕ⁰(x)| = 1

1.5.  Скорость сходимости в методе итераций при нахождении решения нелинейного уравнения

A)  линейная.

B)  квадратичная.

C)  кубическая.

1.6. Прирешениинелинейногоуравненияметодом итераций для остановки вычислений использовать критерий

|xn+1 − xn| < ε

A)  можно не всегда.

B)  нельзя.

C)  можно всегда.

1.7. Формула метода Ньютона решения нелинейного уравнения имеет вид:

A)

B)

C) x_n+1 = x_n − f(x_n)f⁰(x_n), n = 0,1...

1.8. Скорость сходимости в методе Ньютона решения нелинейного уравнения

A)  линейная.

B)  квадратичная.

C)  кубическая.

1.9. Формула метода секущих для нахождения решения нелинейного уравнения имеет вид:

A)

B)

C) x_n+1 = x_n−f(x_n)(x_n − x_n−1)(f(x_n) − f(x_n−1)),              n = 0,1...

1.10. Итерационный процесс при решении системы нелинейных уравнений методом итераций сходится,

A)  есликакая-нибудьнормаматрицыпроизводных меньше 1.

B)  есликакая-нибудьнормаматрицыпроизводных больше 1.

C)  есликакая-нибудьнормаматрицыпроизводных равна 1.

2.1. Формулы Ньютона — Котеса построены

A)  на основе интерполяционного многочлена Лагранжа.

B)  на основе интерполяционного многочлена Ньютона.

C)  с помощью аппроксимации подынтегральной функции константой.

2.2. Формула средних для численного интегрирования построена

A)  на основе интерполяционного многочлена Лагранжа.

B)  на основе интерполяционного многочлена Ньютона.

C)  с помощью аппроксимации подынтеграль ной функции константой.

2.3. Квадратурная формула Гаусса построена

A)  на основе интерполяционного многочлена Лагранжа.

B)  на основе специального выбора весовых коэффициентов общей квадратурной формулы.

C)  наосновеспециальноговыбораузловивесов общей квадратурной формулы.

2.4.  Обобщенная формула трапеций для численного интегрирования имеет вид:

A)

.

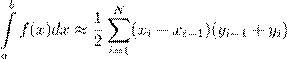B)

.

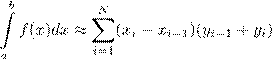C)

.

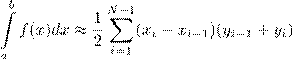2.5.  Погрешность обобщенной формулы трапецийпричисленноминтегрированииопределяется формулой:

A)

,

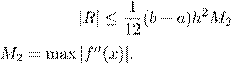где

B)

,

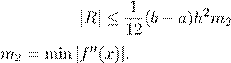где

C)

,

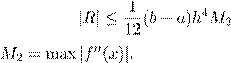где

2.6.  Обобщенная формула Симпсона для численного интегрирования имеет вид:

A)

C)

.

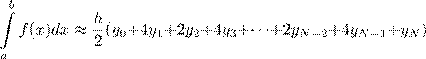2.7.  Погрешность обобщенной формулы Симпсона при численном интегрировании имеет вид:

A)

,

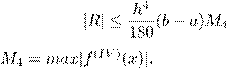где

B)

,

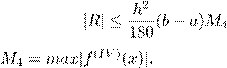где

C)

,

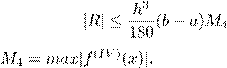где

2.8.  Обобщенная формула средних для численного интегрирования имеет вид:

A)

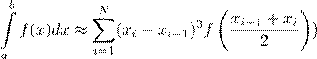
B)

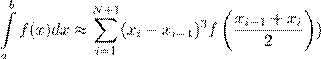
C)

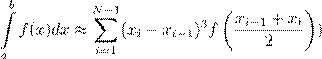
2.9.  На равномерной сетке обобщенная формуласреднихдлячисленногоинтегрированияимеет вид:

A)

. . B) C) .

.

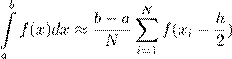2.10.  Погрешность обобщенной формулы сред них при численном интегрировании на равномерной сетке имеет вид:

A)

.

B)

.

C)

.

3.1. Различают следующие основные типы задач для обыкновенных дифференциальных уравнений:

A)  задачаКоши, краеваязадача, задачанасобственные значения.