Таблица всех элементарных булевых функций. Операция склеивания. Операция поглощения

ВВЕДЕНИЕ

Булевой называют функцию f(x₁,x₂…x_n), аргументы которой и сама функция могут принимать два значения. Обозначим множество, составленное из двух элементов, ноля и единицы, буквой Е, Е={0,1}. Областью определения булевой функции f(x₁,x₂…x_n) является совокупность всех перестановок , где .

Поскольку область определения состоит из конечного числа элементов 2ⁿ, то булеву функцию можно задавать при помощи таблицы, например:

 

Х1	Х2	…	Хп-1	Хп	f(x1,x2…xn)
0	0	…	0	0	f(0,0…0,0)
0	0	…	0	1	f(0,0…0,1)
0	0	…	1	0	f(0,0…1,0)
…	…	…	…	…	…
1	1	…	1	0	f(1,1…1,0)
1	1	…	1	1	f(1,1…1,1)

Таблица 2. Таблица всех элементарных булевых функций.

Х1	Х2	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11	F12		F13	F14	F15	F16
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1		1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1		1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0		0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0		1	0	1

Все эти функции от двух аргументов мы и будем называть элементарными булевыми функциями. Семь из них имеют специальные обозначения.

Конъюнкцией называется функция, задаваемая столбцом F₁, обозначается Х₁&Х₂ или Х1Х_2. конъюнкция иначе называется логическим умножением, как наиболее простое используется обозначение Х₁Х₂.

Дизъюнкцией называется функция, задаваемая столбцом F₇. обозначается дизъюнкция Х₁Х₂. другое название дизъюнкции – логическое сложение.

Формулы в базисе   отрицание.

Справедливы следующие тождества:

Будем  называть конъюнкцией любое произведение составленное из букв Х_i, и их отрицаний. Пользуясь тождествами, любую конъюнкцию можно преобразовать либо к нулю, либо к произведению, составленному из букв с различными индексами. Такое произведение называется элементарной конъюнкцией. Формула, имеющая вид (для элементарных конъюнкций) называется Дизъюнктивной Нормальной Формой (ДНФ).

Любую формулу, построенную с помощью знаков дизъюнкции, конъюнкции и отрицания, можно преобразовать к ДНФ.[2]

Булевы тождества можно использовать для упрощения ДНФ.

Рассмотрим три простых способа:

Операция склеивания.

Две конъюнкции  и  склеиваются, т.е. заменяются в ДНФ одной конъюнкцией  , если:  

a)  и  содержат одинаковое множество переменных; б) одна и только одна переменная входит в  и  разнотипно (т.е. в одну с инверсией, в другую без инверсии).

Конъюнкция    получается из   удалением этой разнотипной переменной:

Операция поглощения.

Конъюнкция   поглощает  , т.е.  конъюнкция   может быть удалена из ДНФ, содержащей  , если все переменные   входят в   и   каждая входит в обе конъюнкции однотипно:

                                  Операция неполного склеивания.

Конъюнкции  и  допускают операцию неполного склеивания, если все переменные   входят в  и одна и только одна из них входит в конъюнкции разнотипно. Тогда эта разнотипная переменная может быть удалена из, т. е.

 .[4]

Теорема1:

Каждая булева функция может быть представлена формулой в базисе ().

Доказательство:

Определим булеву степень следующим образом:

                        

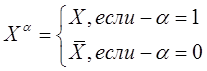
Рассмотрим теперь  произвольную функцию f(x₁,x₂…x_n). Для каждого набора значений переменных , такого, что f(x₁,x₂…x_n)=1, составим конъюнкцию . Относительно этой конъюнкции справедливо утверждение:

=1    при      

=0,         при остальных значениях переменной.

С учетом этого имеем:

.

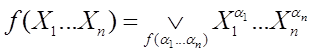Под знаком  записано условие суммирования, оно означает, что сумма распространяется на все наборы , на которых функция равна единице. Правая часть формулы является ДНФ, она называется Совершенной ДНФ (СДНФ) булевой функции.[2]

1.Задача минимизации ДНФ

Определения:

1.  Рангом правильной элементарной конъюнкции называется число разных переменных, входящих в нее.

2.  Рангом ДНФ называется сумма рангов всех элементарных конъюнкций, входящих в ДНФ.

3.  Минимальной ДНФ  для данной функции называется ДНФ, которая равна этой функции и имеет наименьший ранг.

Задача минимизации ДНФ для данной функции состоит в нахождении минимальной ДНФ.

Конъюнкция К называется импликантой функции f, если f = 1 на любом наборе  значений переменных, на котором К = 1.

.

Конъюнкция К называется простой импликантой f, если:

-  К – импликанта f,

-  После вычеркивания из К любой буквы, она перестает быть импликантой.

Теорема 1:

Минимальная ДНФ состоит из простых импликант функции f.

Эту же теорему можно сформулировать так:

Минимальная ДНФ функции f получается из сокращенной, путем удаления некоторых ее членов.

ДНФ составленная из простых импликант функции f, из которой никакую импликанту нельзя удалить так, чтобы оставшаяся ДНФ реализовывала бы функцию f, называется тупиковой.

Таким образом, план минимизация сводится к следующему: найти