Исследование электромеханической следящей системы. Передаточная функция цепи управлений по задающему воздействию

Лабораторная работа № 16 ИССЛЕДОВАНИЕ ЭЛЕКТРОМЕХАНИЧЕСКОЙ СЛЕДЯЩЕЙ СИСТЕМЫ

Цель работы: целью работы является исследование динамических свойств следящей системы, оценка влияния структуры и параметров системы внешних воздействий на ее точностные характеристики.

I. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ПОДГОТОВКЕ К РАБОТЕ

В работе проводится исследование следящей системы, полная структурная

схема которой представлена на рис 1.

Здесь

W_д(p) = k_д  - передаточная функция электромеханического дискриминатора; W_у(p) = k_у- - передаточная функция электронного усилителя;

k^дв - передаточная функция исполнительного ^W_дв(p)= p(Tмp+1)(Toyp+1) двигателя;

W_р(p) = k_р      -передаточная функция редуктора;

 kос p    

W_ос(p) =                  -передаточная функция цепи местной обратной связи;

                 T_э p+1              

ϕ (p) = k_kp - передаточная функция цепи управлений по задающему воздействию;

                                 kм                                    

W_м(p) =− - передаточная функция исполнительного p(T_м p+1)(T_оу p+1) двигателя по моменту;

k_д - коэффициент передачи дискриминатора ( крутизна дискриминационной характеристики); k_у - коэффициент усиления по напряжению усилителя; k_дв - коэффициент передачи исполнительного двигателя; T_м - электромеханическая постоянная времени исполнительного двигателя; T_oу - постоянная времени цепи обмотки управления исполнительного двигателя; k_р - коэффициент передачи редуктора; k_ос -коэффициент передачи цепи местной обратной связи T_ос - постоянная времени цепи местной обратной связи; k_к - коэффициент передачи цепи управления по задающему воздействию; k_м - коэффициент передачи двигателя по моменту .

Как следует из структурной схемы, в системе реализован принцип комбинированного управления - управления по отклонению и по задающему воздействию.

Ошибка системы в установившемся режиме:

V_уст = lim pE(p) = lim p[H_еэ(p)θ₁(p) +H _f (p)M(p)]                       (1)

           p→0                             p→0

Здесь

                                    W ( p)                       

H _еэ ( p) = [1 −ϕ( p)                   ] 1 +W ( p)

                                    W_д ( p)                                                                     (2)

- передаточная функция замкнутой системы по ошибке,

                               W_м(p)                   W(p)      

H _f (p) =                                ^⋅                                                   (3)

W_y (p)W_дв(p)W_д(p) 1+W(p)

- передаточная функция замкнутой системы по моменту нагрузки,

k(1+T_э p)

W(p) =

p(TэTоуTдвp3 +(TоуTэ +TэTдв +TоуTдв)p+(Tоу +Tэ +Tдв)p+1+kуkдвkос)

-передаточная функция разомкнутой системы, k = k_д k_у k_дв k_р – коэффициент передачи разомкнутой системы (без учета местной обратной связи);

Из выражения (1), что система будет инвариантной по отношению к задающему воздействию V₁(t) при Н_еэ (p).

При этом в соответствии с равенством (2) условие полной инвариантности системы

W^д(p)

ϕ(p) =

W(p)

или

                                 ϕ(p) =a₀ +τ₁p+τ₂²p² +...                             (4)

Для систем с астатизмом первого порядка α₀ = 0.

В работе реализуется частичная инвариантность по задающему воздействию за счет введения сигнала Uk(t) = τ₁dV₁ /dt = τ₁pV₁ . 

Этим устраняется скоростная ошибка системы V_ск=Ω/К_Ω что позволяет повысить на единицу порядок астатизма системы [1]. Значение τ₁,как следует из (4), можно определить из выражения kд                           K

                                τ1 =       ,KΩ =

                                        KΩ                       1+ kykдвkос

При управление только по отклонению (ϕ (p)=0) передаточная функция

H_e (p) =

замкнутой системы по ошибке и установившаяся ошибка системы в режиме неподвижного состояния

(V₁(t)=V₁⁰=const) в соответствии с (1)

                                                     kмkр           0      

                                          ^V_уст ^{=  M}                                    (5)

K_Ω

а в режим движение с постоянной скоростью (V1(t)=Ωt)

                                                    Ω      k_мk_{р           0}                            (6)

                                         V_уст =       +         M

                                                   KΩ            KΩ                    

где M⁰ - момент нагрузки двигателя,

Использование управления по задающему воздействию не меняет условий устойчивости системы, так как  вид характеристического уравнения замкнутой системы D(p)=1+W(p)=0 не зависит от структуры и параметров цепи управления по задающему воздействию ϕ (p).

Получить требуемые динамические свойства системы слежения можно за счет изменения параметров местной отрицательной обратной связи k_oc,T_э.

2. ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВИКИ

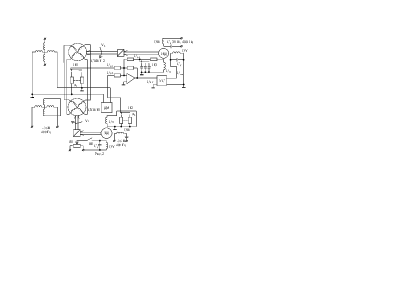
Принципиальная электрическая схема лабораторной установки приведена на рис.2.

Электромеханический дискриминатор реализован на двух синуснокосинусных вращающихся трансформаторах (СКВТ): СКВТ 1 типа ВТ-5 и СКВТ 2 типа 5 ВВТ.

Суммирование сигналов ошибки системы