Исследование основных методов демпфирования систем автоматического управления при использовании последовательных корректирующих цепей

2

ЛАБОРАТОРНАЯ  РАБОТА  № 11

ИССЛЕДОВАНИЕ  МЕТОДОВ  ДЕМПФИРОВАНИЯ

СИСТЕМЫ  АВТОМАТИЧЕСКОГО  УПРАВЛЕНИЯ

Цель работы: исследование основных методов демпфирования систем автоматического управления при использовании последовательных корректирующих цепей.

1. Методические указания по подготовке к работе.

Увеличение точности систем автоматического управления за счет повышения общего коэффициента усиления разомкнутой системы (или добротности) возможно при любых типовых режимах. Однако повышение общего коэффициента усиления ограничивается устойчивостью системы управления и, как правило, оно приближает систему к колебательной границе устойчивости. При некотором значении общего коэффициента усиления K=К_kp , которое называется критическим, в системе возникают незатухающие колебания, то есть она попадает на границу устойчивости. В связи с этим повышение общего коэффициента усиления до значения, при котором обеспечивается повышение требований по точности, обычно производится только при одновременном увеличении запаса устойчивости системы. Это увеличение запаса устойчивости носит название демпфирования.

Демпфирование осуществляется введением так называемых корректирующих устройств (цепей), которые могут включаться в схему системы последовательно, параллельно или в виде специальных обратных связей. В зависимости от свойств корректирующей цепи различают:

-  демпфирование с подавлением высоких частот;

-  демпфирование с подавлением средних частот;

-  демпфирование с поднятием высоких частот (введение положительных фазовых сдвигов);

-  демпфирование с введением отрицательных фазовых сдвигов.

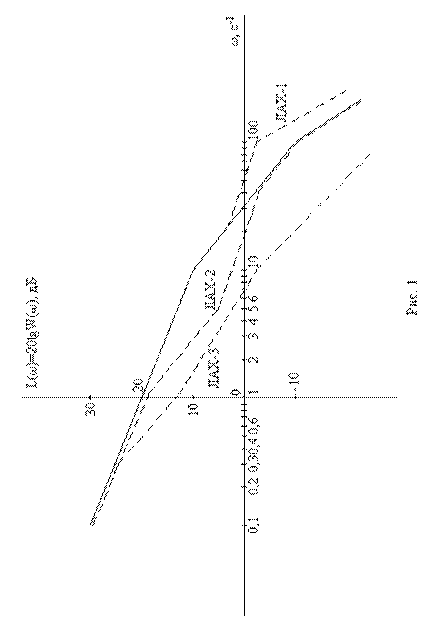
На рис. 1 приведена типовая логарифмическая амплитудная характеристика некорректированной системы (сплошная кривая) и логарифмические амплитудные характеристики системы при различных методах демпфирования (пунктирные кривые).

При демпфировании с подавлением высоких частот уменьшается полоса пропускания и, как следствие, быстродействие системы автоматического управления  (ЛАХ-3 на рис. 1).

Демпфирование с поднятием высоких частот приводит к увеличению быстродействия, но при этом возрастает влияние высокочастотных помех на работу системы (ЛАХ-1 на рис. 1).

положение между этими методами повышения запаса устойчивости (ЛАХ-2 на рис. 1).

В табл. 1 приведены передаточные функции, логарифмические амплитудные характеристики последовательных корректирующих звеньев, используемых для демпфирования систем, и схемы соответствующих пассивных корректирующих цепей, выполненных на RC или RLC элементах.

Следует отметить, что реальные пассивные дифференцирующие цепи имеют коэффициент передачи значительно меньше единицы, и применение их требует значительного усиления в схеме САУ.

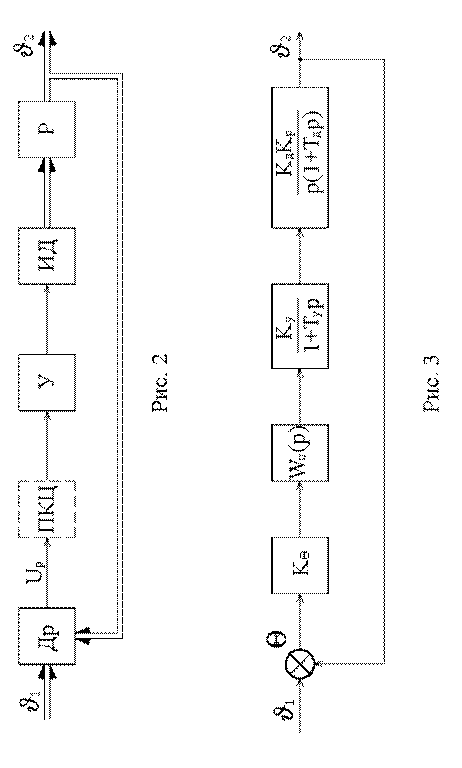
Лабораторная работа посвящена изучению основных методов демпфирования на примере следящей системы воспроизведения угла (слежения по углу), упрощенная схема которой показана на рис. 2, где обозначены:

ДР - датчик угла рассогласования,

У - усилитель,

ИД - исполнительных двигатель, Р - редуктор,

ϑ₁- угол поворота командной (входной) оси, ϑ₂ - угол поворота исполнительной (выходной) оси,

U_p- напряжение, поступающее с датчика угла  на вход усилителя следящей системы,

ПКЦ - последовательная корректирующая цепь.

Если все элементы следящей цепи считать линейными, то ее структурная схема может быть изображена в виде, показанном на рис. 3, где k_ϑ,k_y,k_d,k_p - коэффициенты передачи датчика рассогласования, усилителя, исполнительного двигателя и редуктора соответственно; T_y - постоянная времени усилителя; T_d - электромеханическая постоянная времени исполнительного двигателя и  ϑ= −ϑ₁ ϑ₂- угол рассогласования.

Передаточная функция разомкнутой исходной (некорректированной) системы в соответствии со структурной схемой будет:

                             W_p(p) =^ϑ2(p⁾ =              K^Ω                                                                          (1)

                                        ϑ(p)      p(1+T_d p)(1+T_y p)

где K_Ω =k_ϑk_yk_dk_p , 1/c - добротность следящей системы по скорости. В настоящей работе принято, что нам известны постоянные времени T_d и T_y и коэффициенты передачи k_y,k_d,k_p . Таким образом, единственным варьируемым параметром в некорректированной системе является коэффициент передачи датчика рассогласования k_ϑ и, соответственно, добротность по скорости K_Ω.

                                                                  5                                                                                                                                               6

В следящей системе с астатизмом первого порядка добротность по скорости однозначно определяется требованиями, предъявляемыми к точности слежения, и может быть вычислена по формуле:

Ω^M

                                                                                                                                                                                                  K_Ω =                                                                                                                                                                               (2)

ϑΩ

где  Ω_M - максимально возможная скорость вращения командной оси - скорость слежения; ϑ_Ω- максимально допустимая величина рассогласования (скоростной ошибки).

Воспользовавшись критерием Гурвица, нетрудно убедиться в том, что в рассматриваемой системе добротность по скорости ограничена сверху величиной:

                                                                                                                                                                                                  K_kp = ¹ + ¹                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                          (3)

                                                                                                                                                                                                                   Td Ty

В результате при выборе добротности следящей системы в соответствии с формулой (2) запас устойчивости системы окажется недостаточным, а при K_Ω >K_kp система вообще будет неустойчивой.

Например, при T_d = 0,1с и  T_y =0,01с добротность по скорости будет равна K_kp = 110c⁻¹. Если  заданы Ω_M = 60 град/с и  ϑ_Ω= 12 угл. мин., требуемое значение

K_Ω = 300c⁻¹, что больше критического коэффициента усиления, следовательно, система будет неустойчива.

Для обеспечения необходимой величины запаса устойчивости замкнутой системы при одновременном выполнении требований к точности в состав следящей системы можно ввести последовательную корректирующую цепь (ПКЦ). Она показана на рис. 2 и 3 пунктиром. Передаточная функция разомкнутой системы (скорректированной) будет определяться формулой согласно (1):

                                                                                                                                                                                                                                           K^Ω W p( )

        W_ck = W_p ( )p W p( ) = p(1+ T p_d )(1+ T p_y )

Дальнейшая задача состоит в том, чтобы определить необходимую