Влияние объема и формы блоков РЭС на показатели качества конструкции. Зависимость вариации мощности рассеяния блока от вариации его объема

Влияние объема и формы блоков РЭС

на показатели качества конструкции

В зависимости от назначения , уровня интеграции и объекта установки объем  форма блоков РЭС могут быть различными : объем обычно меняется от одной десятой до нескольких десятков кубических дециметров , а форма может быть плоской , кубической , прямоугольной или цилиндрической.

От этих двух параметров конструкций блоков в сильной степени зависят такие показатели качества , как допустимая удельная мощность рассеяния (тепловая напряженность ) и вибропрочность , во многом определяемая собственной частотой конструкции . Как качественно влияют первые на вторые , известно каждому конструктору: конструктив с меньшим объемом допускает большую тепловую напряженность , чем конструктив  с большим объемом ; конструктив более плоской формы способен выдержать большую мощность рассеяния , чем куб при равенстве объемов , а показатели вибропрочности при этом будут на много хуже. Это, казалось бы, подтвердить и с помощью формул. Например , удельная мощность рассеяния Р_{уд.расс}  = Р_расс / V должна зависеть обратно пропорционально от объема , и поэтому если кристалл ИС с объемом в 1 мм³ способен рассеивать 40 мВт , т.е.  Р_{уд.рассИС} = 40 * 10³ Вт/дм³ , то блок РЭС , имеющий объем 1 дм³  , т.е. в 10⁶ раз больший , должен иметь допустимую тепловую напряженность всего 0.04 Вт/дм³ . Результаты же эксперимента , приведенные в работе [16]  , дают значение этой величины 10 Вт/дм³ , т.е. в 250 раз больше. Значит , формальный расчет по указанной формуле нреален, ошибочен.

Поэтому для конкретных конструкторских разработок необходимо иметь более строгие количественные оценки этого влияния , учитывающие все факторы , в том числе и форму блоков.

Оценим влияние объема блока на удельную мощность рассеяния , считая для простоты выводов форму блока со стороной  а_б кубической.

Изменение стороны куба в к₁ раз приведет к изменению его объема в  . Поскольку площадь поверхности кубы , а объем  , то удельная мощность рассеяния

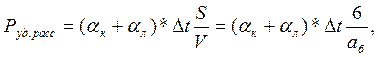
где  -  коэффициенты теплопередачи конвекцией к лучеиспусканием от блока в среду ;  - перегрев корпуса блока. Если принять какой – либо объем блока за номинальный , например , и по отношению к нему оценить изменение (вариацию) удельной мощности рассеяния  В_р при изменении (вариации) объема В_v (в  раз) для i – го варианта , то такая оценка может быть проведена по следующей формуле :

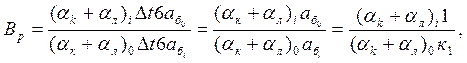                            (1)

где  - стороны для номинального объема и i – го варианта .

С изменением стороны куба (определяющего размера) коэффициент лучеиспускания не меняется ; коэффициент конвекции для закона степени ¼ , как показывают расчеты , меняется незначительно (5…10%), а для степени 1/3  не меняется . Поэтому выражение  (1) можно записать в виде В_р = 1/ k_i . Зависимость В_р = f(B_v), где B_v = V_i / V₀ =  , построенная по точкам , представлена на рис. 1.

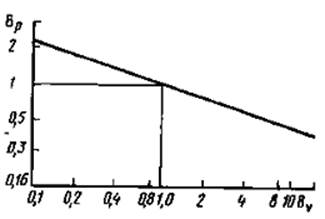
Рис.1 Зависимость вариации мощности рассеяния блока от вариации его объема

Из графика видно , что при изменении объема в 10 раз в сторону увеличения или уменьшения удельная мощность рассеяния , в том числе и допустимая , изменяется лишь в два раза (а не в 10 раз) в обратную сторону. Этим и объясняется ошибка в оценке возможных изменений допустимой тепловой напряженности по общей формуле, так как главным фактором является не сам объем , а отношение площади теплопередачи к объему , т.е. S / V . Поэтому для практических расчетов на рис. 2 приведена  зависимость этого отношения от объемов блоков РЭС.

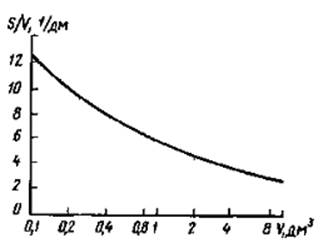
Рис.2.  Зависимость отношения площади теплоотдачи блока к его объему от объема блока

Оценим количественное влияние формы блока на удельную мощность рассеяния. Для этого кубическую форму блока будем либо “вытягивать” в столбик , либо “сжимать” в более плоскую (планарную) пластину. Второй случай на практике более реален, причем пластина может иметь как квадратную , так и прямоугольную формы. Для простоты выводов выберем квадратную форму плоского блока – панель. Введем понятие коэффициента планарности , отражающего степень плоскости конструкции , как к₂ = а_б / h^’ , где а_б – сторона куба , h^’ – высота панели (рис. 3).

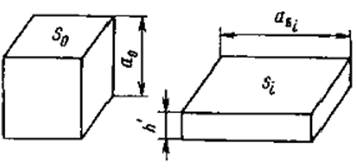
Рис.3. К определению коэффициента планарности конструкции блока

При этом объемы куба и панели равны. Откуда а _б * S ₀ = h’ * S _i  и k₂ = S _i / S ₀ . Поскольку  S_i > S₀ , то при увеличении коэффициента планарности должна возрасти допустимая мощность рассеяния в блоке , так как с большей площади теплоотдачи в среду может быть передана большая мощность рассеяния.

Оценим это количественно. Обозначим увеличение стороны верхней грани панели через  к₃ =  а_бi / а_б . Тогда общая площадь теплоотдачи панели

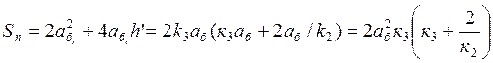
Из равенства объемов находим , что   и 

Заменим  к₃ на к₂ в выражении для площади , получим 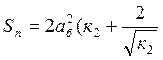 . Увеличение удельной мощности рассеяния В’_p за счет перехода