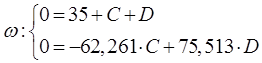
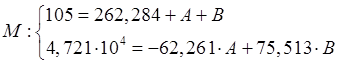
Решая систему находим значения коэффициентов:
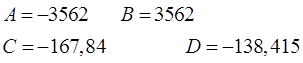
Тогда окончательно решение имеет вид:
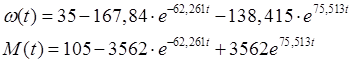
Графики переходных процессов представлены на рис. 8.
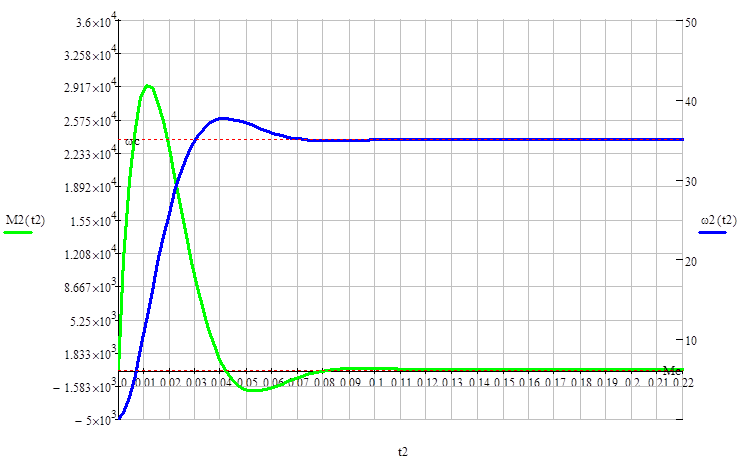
Рис. 8. Второй этап переходного процесса.
Переходные процессы замкнутой системы.
Рассмотрим переходной процесс пуска до пониженной скорости.
I этап: M
Mc = 105 Н∙м. Протекает электромагнитный процесс. При этом якорь
неподвижен (ω=0), сигнал обратной связи по скорости отсутствует и Koc
= 0, Кот = 0. Данный этап аналогичен первому этапу переходного
процесса разомкнутой системы и имеет вид, представленный на рис. 9.
|
|
Рис. 9. Первый этап переходного процесса.
II этап: 
. Якорь ЭД начинает разворачиваться, при этом: 
, 
. Начальные условия ω(0) = 0, M(0) = Mc, а начальные значения производных соответственно
равны:
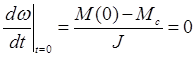
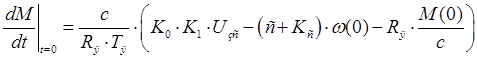
Решается данная система аналогично тому, как решалась подобная для разомкнутой системы. Переходной процесс длится до тех пор, пока момент не достигнет значения момента уставки. Вид переходного процесса представлен на рис. 10.
Конечные значения переменных на данном этапе:
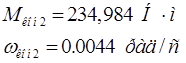
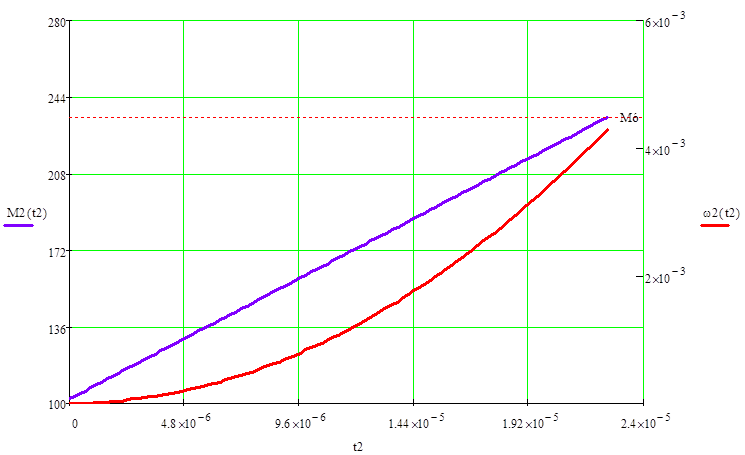
Рис. 10. Второй этап переходного процесса.
III этап: 
. Включена обратная связь по току: Koc ≠
0, Кот ≠ 0. Начальные значения переменных ω(0) = ωкон2,
М(0) = My, а начальные значения производных
определяются аналогично, как и для предыдущего этапа, но с учетом действия
обратной связи по току. Временные диаграммы скорости и момента показаны на рис.
11.
Этап заканчивается в момент времени t3 при достижении моментом значения My, а скорость ωкон3.
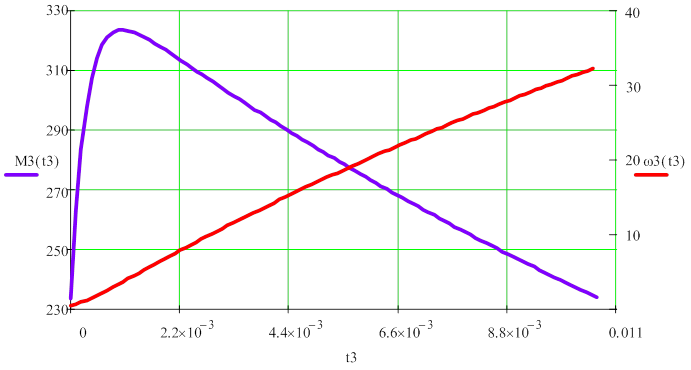
Рис. 11. Третий этап переходного процесса.
IV этап: 
. Обратная связь по току отключена и Кот
= 0. Начальные условия для данного этапа ω(0) = ωкон3, М(0) =
My. Значения производных определяются, как и в
предыдущих случаях. Диаграммы для IV этапа
представлены на рис. 12. Этап заканчивается в момент времени t3 при достижении моментом значения Mс=102Нм, а скорость ωс =35 рад/с.
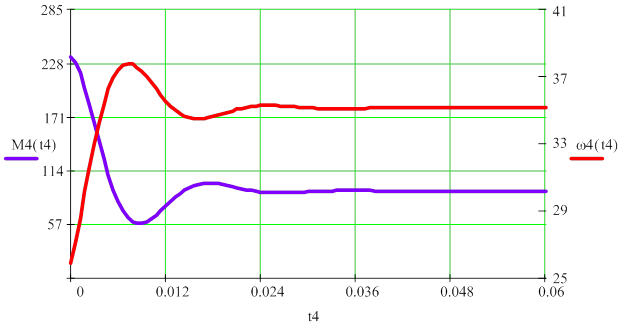
Рис. 12. Четвертый этап переходного процесса.
При
припасовывании результатов каждого этапа получаем характеристики 
и 
для всего
процесса пуска (рис. 13 а,б).
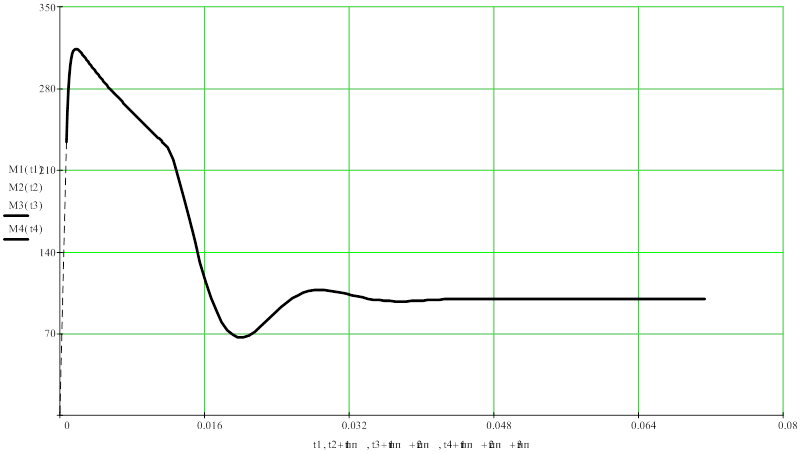
Рис. 13 а. Общий п.п. по электромагнитному моменту электродвигателя.
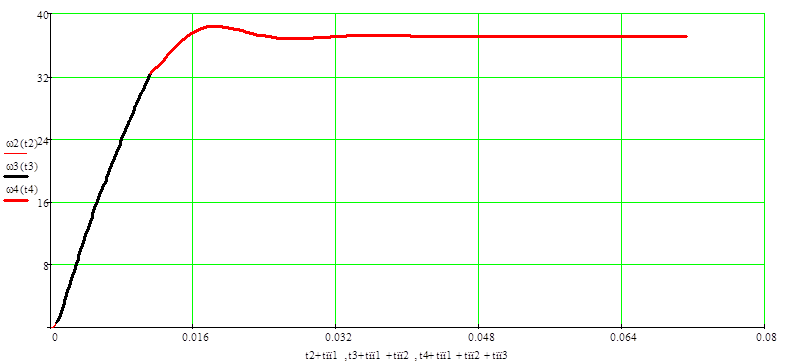
Рис. 13 б. Общий п.п. по скорости электродвигателя.
На рисунке 14 представлены статическая и динамическая характеристики двигателя.
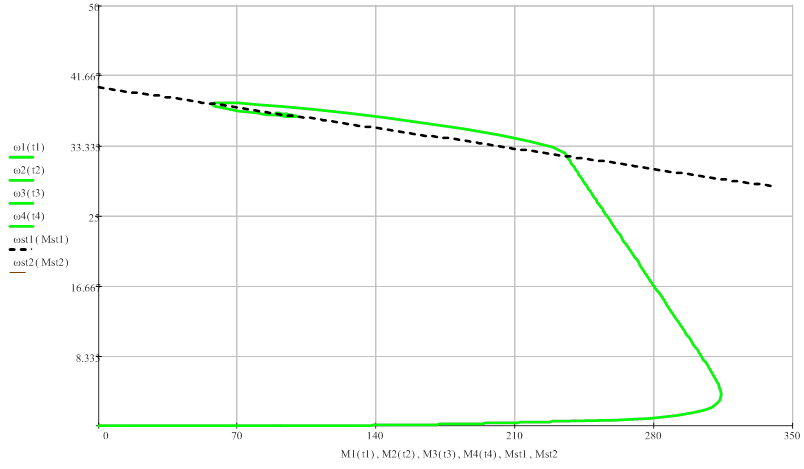
Рис. 14 Статическая и динамическая характеристики замкнутой системы
Переходные процессы за весь цикл работы.
Расчет переходных процессов за весь цикл работы будем производить в MatLab Simulink.
Рассчитаем п.п. для всего процесса: пуск ЭД на холостом ходу, наброс нагрузки, резание, сброс нагрузки, холостой ход, реверс, обратный ход стола, торможение и отключение.
Вид п.п. по скорости и по моменту представлен на рис. 15 и 16 соответственно.
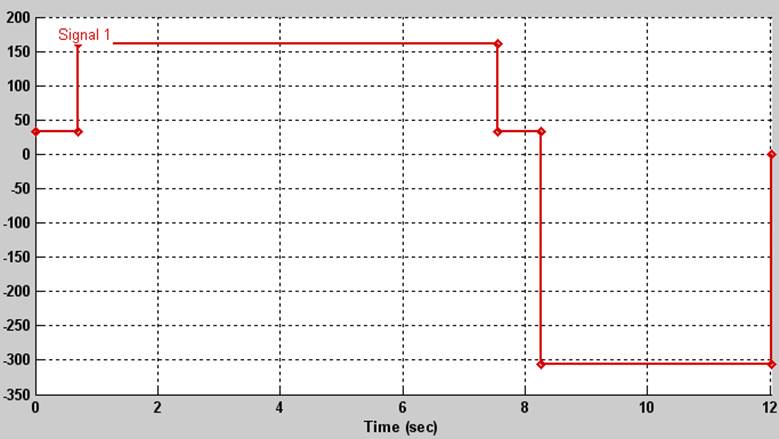
Рис. 15. Диаграмма п.п. при задании скорости.
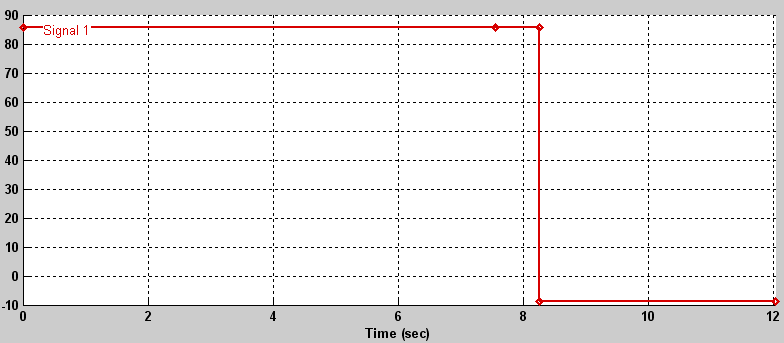
Рис. 16. Диаграмма п.п. при задании статического момента
Система уравнений, описывающая систему:
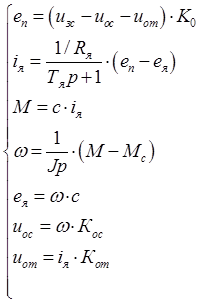
Структурная схема MatLab, соответствующая системе представлена на рис. 17.
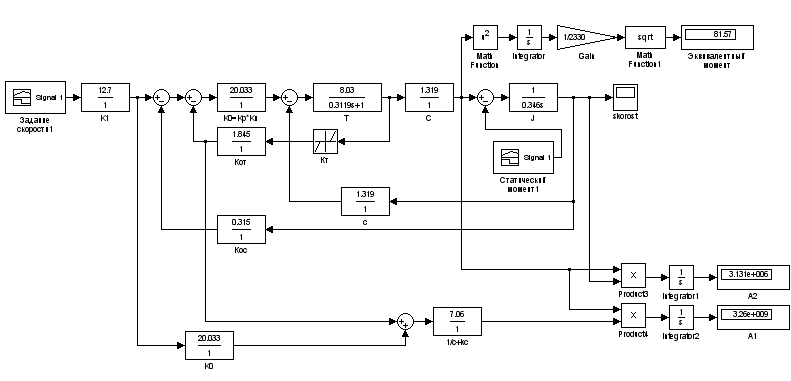
Рис. 17. Структурная схема MatLab описывающая систему.
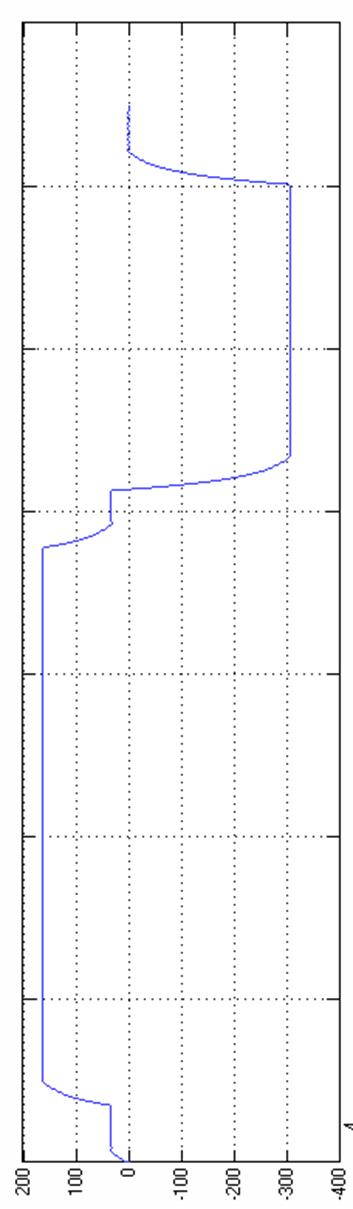
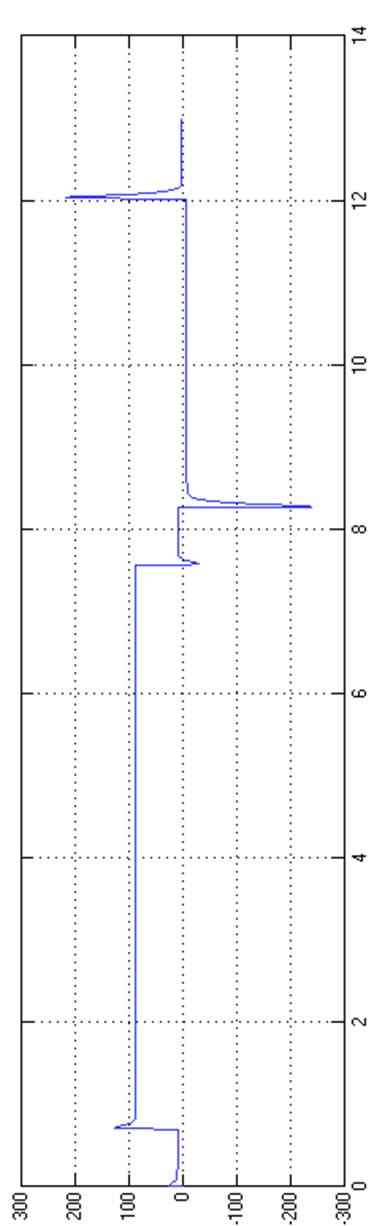
Переходные процессы по скорости и моменту имеют вид, представленный на рис. 18 и 19.
9. Окончательная проверка электродвигателя.
Проверку двигателя по нагреву проведем с помощью метода эквивалентного момента. Расчет производим согласно выражению:
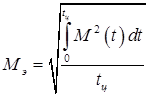
Расчет эквивалентного момента также проводим в MatLab Simulink.
Рис. 20. Фрагмент модели ЭП в MatLab Simulink, реализующий расчет эквивалентного момента.
Эквивалентный момент меньше номинального момента двигателя, поэтому делаем вывод, что двигатель проходит по нагреву.
Mэ = 81,57 < Mн = 105,973
Из
диаграммы переходного процесса момента видно, что максимальное значение момента
Mmax = 
Н∙м.
Максимальный момент двигателя, исходя из перегрузочной способности, равен:
Mmax.дв = λI ∙Mн = 1.5∙105,973 = 158,959 Н∙м
Поэтому делаем вывод, что двигатель так же проходит и по перегрузочной способности.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
