Зарядные цепи с индуктивно-емкостными преобразователями, страница 4

где — максимальное значение из формул (1.66) и (1.90) при или, что то же, при , определяемом по фор­муле (1.73).

    Отсюда получаем, что при  относительная пиковая мощность зарядной цепи с Г-образным ИЕП

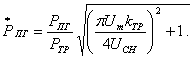                                               (1.125)

     Здесь величина Р_тр берется по формуле (1.105). При минимизации суммарной  установленной  мощности  элементов  ИЕП  и  выборе по формуле (1.109) имеем

     Для зарядной цепи с Т-образным ИЕП при  и  и не зависит от величины k_тр.

     По уровню пиковой   мощности   предпочтение   следует   отдать Т-образной схеме, обеспечивающей выигрыш по этому важному параметру в 1,615 раза по  сравнению  с  зарядной цепью  на  базе Г-образного   ИЕП (см. рис. 20, а).

     Уточненный анализ зарядной цепи с од­нофазным Г-образным ИЕП. Проведенный анализ является упрощенным, так как мы рассматривали процессы в за­рядных цепях с ИЕП в традиционном линейном приближении, когда все токи и напряжения на элементах ИЕП синусоидальны. В действительности наличие заряжаемой батареи конденсаторов, подключенной к ИЕП через выпрямительный мост, приводит к усложнению процессов и появлению ряда важных особенностей, которые не могут быть выявлены при анализе линейной цепи.

       В качестве примера исследуем зарядную цепь с Г-образным ИЕП, изображенную на рис. 20, а, и проанализируем процессы, с учетом влияния вентильного моста и батареи конденсаторов С.При этом ограничимся случаем длительной зарядки, когда на ин­тервале одного полупериода напряжение на батарее конденсато­ров U_с практически не изменяется и анализ процессов на каждом из полупериодов можно проводить, считая, что вместо батареи кон­денсаторов в схему включена противо-ЭДС.

Принимая, что трансформатор Тр идеален и С → ∞, получаем эквивалентную схему, изображенную на рис. 27, а, где U'с = Uс/k_тр — приведенное к первичной обмотке трансформатора напряжение на батарее конденсаторов. В рассматриваемом случае на каждом из полупериодов процесса зарядки изменением U'_с можно пренебречь и полагать U_с = const. При этом в полувол­не тока можно выделить два интервала, на каждом из которых раз­личие в процессах обусловлено различием структур эквивалент­ных схем. На интервале / эквивалентная схема имеет структуру, представленную на рис. 27, б, модуль напряжения на конденсаторе С₀ меньше напряжения U'_с и нагрузка с выпрямителем не влияет на характер переходных процессов. На интервале // схема замещения имеет вид, показанный 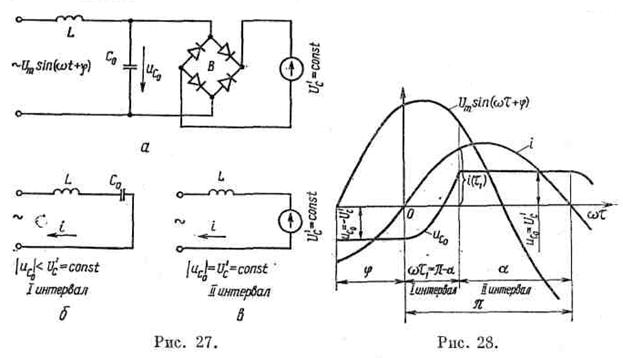на рис. 27, в  конденсатор С₀ не влияет на характер переходных процессов (С₀ << С). Кривые изменения тока i, потребляемого из сети, и напряжения на конденсато­ре С₀ на одном из полупериодов процесса зарядки приведены на рис. 28.

      Обозначим угловую величину интервала II через α, тогда уг­ловая величина интервала I  будет равна π-α. Рассмотрим про­цессы на интервале I. Условимся время τ отсчитывать от момента прохождения тока i через нуль, а угол сдвига между напряжением сети и током i обозначим через φ. Потребуем также, чтобы соблю­далось основное для элементов ИЕП условие: . Гранич­ные условия для рассматриваемого интервала имеют вид:

                                              (1.126)

Решение дифференциального уравнения

                                   (1.127)

описывающего процессы в схеме рис. 27, б, при приведенных выше граничных условиях и  имеет вид

                (1.128)

откуда

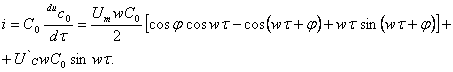        (1.129)

      Учитывая, что при  значение  и , из уравнений (1.128) и (1.129) после преобра­зований получаем

                                      (1.130)

                         (1.131)

На интервале II процессы в схеме, изображенной на рис. 27, в, описываются уравнением

                                           (1.132)

откуда при

                              (1.133)

При  Подставив эти значения в уравнение (1.133) с учетом, что  и , после преобра­зования найдем

                                    (1.134)

Совместное решение уравнений (1.130), (1.131) и  (1.134)  поз­воляет установить связь между углами φ и α:

           (1.135)

Эта зависимость построена на рис. 29. При  В начале зарядки в случае  и φ=π/2, по мере воз­растания напряжения на батарее конденсаторов α и φ умень­шаются, стремясь к нулю при .

Поскольку ток  идет на зарядку батареи конденсаторов только на интервале II при  и весь ток явля­ется зарядным током в случае принятых выше допущений (иди ра­боте на противо - ЭДС ток через конденсатор С₀ на интервале II не течет), то среднее за полупериод значение зарядного тока  , приведенное к первичной обмотке согласующего трансформатора, может быть рассчитано по формуле

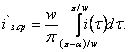
Подставив сюда значение из уравнения (1.133) и использовав, выражение (1.134), после интегрирования придем к следующему ре­зультату, который можно представить в безразмерном виде:

 

                                                          (1.137)

Из рассмотрения уравне­ний (1.130), (1.535) и (1.137) следует, что , ибо параметры φ и α  могут бать исключены при

трех уравнений. Зада­ваясь рядом значений а и поль­зуясь этими тремя уравнения­ми, можно рассчитать значения  и , соответствующие каждому из значений α, и

по­строить кривую, изображенную на рис. 30. Видно, что в рассмат­риваемом случае при работе ИЕП

на выпрямитель, к выходу которого подключена батарея конденса­торов, зарядка не осуществляется неизменным током. Зарядный ток уменьшается по мере повышения напряжения на конденсаторах

2     и_т                                             .1

от значения  в начале  зарядки до     в  конце   зарядки  и  неизменным   его   можно   считать лиш при  , когда устройство работает в режиме частичной подзарядки.

     Однако, как показано при анализе схем с Г-образным ИЕП, оптимальные значения отношения  лежат между 0,55 и 1,04 и при зарядке от  с изменением зарядного тока в процессе зарядки необходимо считаться.