Зарядные цепи с индуктивно-емкостными преобразователями, страница 2

       Величина  зависит   от   коэффициента   трансформации    и принимает минимальное значение, если

                                                        (1.81)

При выполнении этого условия

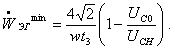                                                   (1.82)

       Если условие оптимизации не соблюдается, то энергоемкость элементов ИЕП может возрасти в десятки раз. Поэтому в заряд­ных цепях с ИЕП необходимо применять согласующий трансфор­матор за исключением случаев, когда величина получается близкой к единице.

       Анализ полученных выражений показывает, что с возрастани­ем U_Co энергоемкость элементов ИЕП линейно уменьшается. За­рядные цепи с Г-образной схемой ИЕП имеет смысл использовать при процессе зарядки, охватывающем достаточно большее число полупериодов напряжения   сети.  Так,  например,   при   и  В случае  соблюдения условия минимизации (1.81) имеет место равенство энергоемкостей элементов ИЕП: .

      Если нас интересует минимизация веса элементов ИЕП, то вве дя величины [кг/Дж] и у_с [кг/Дж], которые представляют собой массу накопителя данного типа, приходящуюся на один джоуль накопленной энергии, и принимая допущение, что в рас­сматриваемом ограниченном интервале варьирования энергий и величины  и у_с практически не изменяются, получаем выражение    для    упрощенной    оценки    весовых    характеристик элементов ИЕП в безразмерной форме:

                               (1.83)

Минимум выражения (1.83) наблюдается в случае

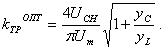                                                  (1.84)

      При этом и

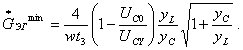                                        (1.85)

       Аналогичные выражения получаются для относительной стои­мости элементов ИЕП:

                    (1.86)

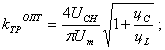                                                                                                          (1.87)

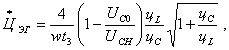                                              (1.88)

где ц_L и ц_C [руб/Дж] - стоимость материалов, приходящихся па один джоуль

накопленной энергии в реакторе и конденсаторах соответственно. Полученные формулы носят оценочный характер, так как было принято допущение, что у_с и ц_с одинаковы для накопителя С и конденсатора С₀.

       Таким образом, применение согласующего трансформатора позволяет изменять соотношения весов, стоимости и энергоемкости элементов в Г-образной схеме ИЕП. При оптимально выбранном коэффициенте трансформации можно добиться получения ми­нимума либо стоимости, либо веса, либо энергоемкости ИЕП в за­висимости от поставленных перед проектировщиком требований. Величина не зависит от начального напряжения на батарее конденсаторов.

       Оптимальным следует считать вариант выполнения зарядной це­пи, характеризующейся минимумом суммарного веса элементов ИЕП и согласующего трансформатора, либо минимумом суммарной стоимости элементов ИЕП и согла­сующего трансформатора.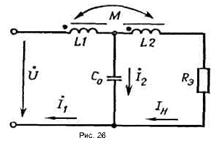

     Анализ зарядной цепи с однофазным Т-образным ИЕП в линейном приближении. Рас­смотрим зарядную цепь, изобра­женную па рис. 23. Ее схема за­мощения представлена на рис. 26. Примем, что индуктивности реак­торов L1 и L2 одинаковы и равны L, коэффициент связи между обмотками реакторов k_с = М/L =1, активное сопротивление обмоток реакторов L1 и L2 равно нулю, . При этом, как показано в работе [49], токи в ветвях схемы замещения

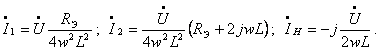                        (1.89)

     Амплитуды токов соответственно равны

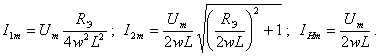                        (1.90)

     Формулы (1.68) - (1.73) остаются в силе и для рассматриваемой зарядной цени с Т-образным ИЕП. Однако, так как здесь

                                                        (1.91)

индуктивность L получается в два раза меньше,   а  емкость С₀ в два раза больше, чем в зарядной цепи с Г-образным ИЕП:

                                                     (1.92)

                                                     (1.93)

     Использовав формулы   (1.73),   (1.76),   (1.90), (1,92)   и (1.93), нетрудно показать, что в этом случае при

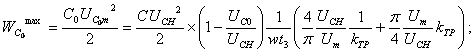                           (1.94)

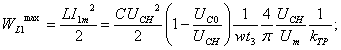                                 (1.95)

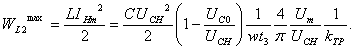 (1.96)

Здесь все энергии выражены через основные параметры U_т, U_С0, Uс_H, w, t₃, и С. Такая форма записи позволяет сравнить различ­ные зарядные цепи при одинаковых условиях зарядки.

       Для зарядной цепи, изображенной на рис. 23, относительная энергоемкость  элементов   ИЕН

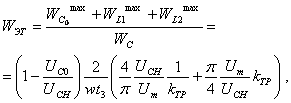                                 (1.97)

где Поскольку токи в реакторах L1 и L2 сдвинуты на   угол π/2,   энергоемкости   и должны  учитываться независимо. Относительная   энергоемкость    в  рассматривае­мой схеме минимальна при

                                                                 (1.98)

Величина не зависит от . При оптимальном коэффициенте трансформации

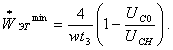                                                          (1.99)

       Из сравнения выражения (1.99) с (1.82) видно, что энергоем­кость элементов ИЕН в зарядной цепи с Т-образной схемой ИЕП в  раз меньше энергоемкости элементов в зарядной цепи с Г-образной схемой ИЕП. При выполнении условий минимизации и . Очевидно, что и в зарядных цепях с Т-образными ИЕП введение согласующего трансфор­матора является обязательным за исключением случаев, ког­да величина , определяемая по формуле (1.98), близка к единице.

       Анализ условий, при которых наблюдается минимум веса или стоимости элементов ИЕП, может быть проведен так же, как это было сделано для зарядной цепи с Г-образным ИЕП.

      Оказывается, что для зарядной цепи с Т-образным ИЕП при  минимумы энергоемкости, веса и стоимости элементов ИЕП наблюдаются при одном и том же значении коэффициента трансфор­мации определяемом но формуле (1.98). При этом относитель­ный вес элементов ИЕП

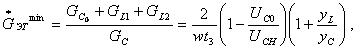                            (1.100)

относительная стоимость элементов

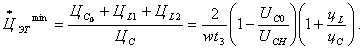                            (1.101)

Сравнение основных технико-экономических характеристик зарядных цепей с Г- и Т - образными ИЕП. Сравнение формул (1.100) и (1.101) с формулами (1.85) и (1.88), полученными для Г-образной схемы ИЕП, приводит к отношениям