Зарядные цепи с индуктивно-емкостными преобразователями, страница 3

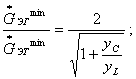
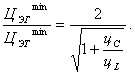                                           (1.102)

Отсюда следует, что при  и равенстве ипдуктивностей ре­акторов L1 и L2 Т-образную схему ИЕП целесообразно при­менять в однофазных зарядных цепях, если  или , в противном случае предпочтение необходимо отда­вать Г-образной схеме. Однако если реакторы L1 и L2 выполнены с различными индуктивностями L1 и L2 и коэффициент отличен от единицы, то технико-экономические характе­ристики, зарядной цепи с Т-образной схемой ИЕП зависят от вели­чины коэффициента . Эти характеристики можно улучшить, изменяя величину  и получая самые различные соотношения между весовыми и стоимостными показателями реакторов и кон­денсатора С₀. Более подробные сведения по этому вопросу можно найти в работах [48, 130, 139].

     Полученные выше формулы позволяют определить действую­щее значение токов и другие энергетические характеристики заряд­ных цепей с Г- и Т-образными ИЕП. Так, например, при длитель­ных процессах зарядки, когда токи в ветвях можно считать сину­соидальными с медленно изменяющейся во времени амплитудой, действующие значения  токов  можно  определять по формуле

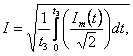
                                              (1.103)
где  - медленно изменяющаяся во времени амплитуда.

       Выражения для - получаются из формул (1.66) и (1.90) после подстановки в них значения  из (1.71) и значений  из (1.74) либо (1.92). При для зарядной цепи с Г-образ­ной схемой ИЕП имеем действующие значения токов

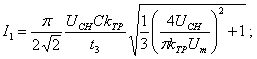
                              (1.104)

      Типовая (габаритная) мощность согласующего трансформатора

                                                 (1.105)

где  - наибольшее значение по формуле (1.70) при  .

     Наибольшее значение напряжения на обмотке реактора  при

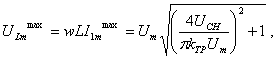                                    (1.106)

откуда относительная типовая мощность реактора

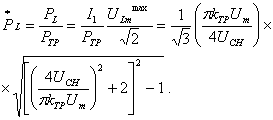                                        (1.107)

      Относительная установленная мощность конденсатора С₀ оп­ределяется по формуле

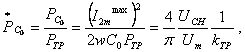                                      (1.108)

где   значение берется  по формуле   (1.66) при   и ; значения и С₀ — из формул (1.74) и (1.75).

     Из выражений (1.107) и (1.108) следует, что минимум   суммарной  установленной  мощности  элементов   ИЕН наблюдается,   когда

                                                      (1.109)

     При этом

              (1.110)

     Минимум относительной типовой мощности реактора имеет место, если

                                                            (1.111)

    В этом случае

                          (1.112)

   Последний вариант уступает варианту с минимальной суммар­ной установленной мощностью элементов ИЕП, так как мощность конденсаторов возрастает почти вдвое, тогда как мощность реакто­ра уменьшается незначительно.

   Аналогично для однофазной зарядной цепи с Т-образной схемой ИЕП  получаем  :

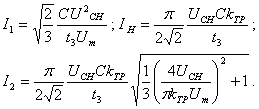                                                      (1.113)

       Для типовой мощности согласующего трансформатора и в этом случае справедлива формула (1.105), а для относительной установленной мощности конденсатора С₀ — формула

(1.114)

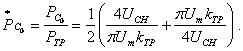                                           (1.114)

        Примем, что схема содержит двухобмоточный реактор с одним магнитопроводом, индуктивности обмоток  и одинаковы и равны , коэффициент связи между обмотками к_с = М1= 1, коэффициент трансформации между обмотками реактора . Определим типовую мощность двухобмоточного реактора со сталью при этих допущениях.

       Для рассматриваемой схемы согласно формулам (1.89) токи  и сдвинуты на угол π/2, поэтому для максимального значения потокосцепления при и  справедливо выра­жение

                                                 (1.115)

где амплитуды токов  и определяются но формулам (1.90); —наибольшее значение амплитуды тока  при . Сечение меди реактора при числах витков обмоток  будет

                                                       (1.116)

Здесь — плотность тока; и — действующие значения токов в обмотках реактора.

      Для определения типовой мощности двухобмоточного реактора  воспользуемся  формулой

                   (1.117)

Подставляя сюда значения , , , и  из формул (1.92), (1.113), (1.90) при значении  из (1.73) и, получаем  в  безразмерном   виде

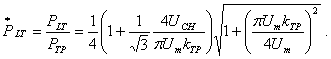                       (1.118)

      Из   рассмотрения   выражений   (1.114)   и   (1.118)   следует,   что минимум величины можно получить, выбрав по формуле (1.98). При этом

                           (1.119)

     Минимум относительной типовой мощности реактора достигает­ся, если

                                                  (1.120)

В этом случае

                           (1.121)

     Минимальная суммарная мощность всех элементов ИЕП имеет место при

                                                      (1-122)

В последнем случае

                     (1.123)

     Все перечисленные варианты весьма близки между собой. Пред­почтение можно отдать варианту с минимальной суммарной мощ­ностью элементов ИЕП, которая в 1,647 раза меньше, чем в заряд­ной цепи с Г-образным ИЕП (см. рис. 20, а). Однако здесь следует учитывать то обстоятельство, что установленная мощность конденсаторовв   зарядной

цепи с Г-образным ИЕП в   1,269 раза меньше в схеме с Т-образным ИЕП, если в последней k₂₁ = 1 и k_с = 1. Этот показатель в схеме с Т-образным ИЕП можно улуч­шить, изменяя величину k₂₁. При этом можно получить практиче­ски любое соотношение установленных мощностей конденсатора С₀ и реактора. Более подробно останавливаться на роли коэффи­циента k₂₁ не имеет смысла, поскольку все сведения по этому воп­росу можно найти в работах [48, 136, 139].

    Определенный интерес представляет сравнение пиковой мощ­ности, потребляемой из сети в конце процесса зарядки в однофаз­ных зарядных цепях с Г - и Т-образным ИЕП. Для обеих схем пи­ковая мощность может быть рассчитана по формуле

                                                 (1.124)