Модель рыбной отрасли. Построение модели рынка. Математическая модель рынка с четырьмя потребителями и производителями

Модель рыбной отрасли

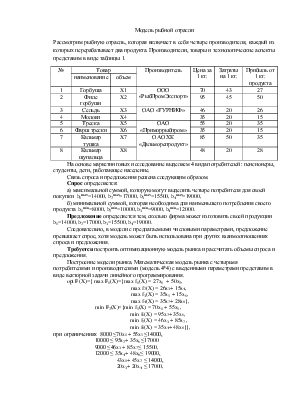
Рассмотрим рыбную отрасль, которая включает в себя четыре производителя, каждый из которых перерабатывает два продукта. Производители, товары и технологические аспекты представим в виде таблицы 1.

На основе маркетинговых исследование выделяем 4 вида потребителей: пенсионеры, студенты, дети, работающее население.

Связь спроса и предложения решена следующим образом.

Спрос определяется:

а) максимальной суммой, которую могут выделить четыре потребителя для своей покупки  b₁^max=14000, b₂^max=17000, b₃^max=15500, b₄^max=19000, б) минимальной суммой, которая необходима для наименьшего потребления своего продукта  b₁^min=8000, b₂^min=10000, b₃^min=9000, b₄^min=12000.

Предложение определяется тем, сколько фирма может изготовить своей продукции  b₁=14000, b₂=17000, b₃=15500, b₄=19000.

Следовательно, в модели с предлагаемыми числовыми параметрами, предложение превышает спрос, хотя модель может быть использована при других взаимоотношениях спроса и предложения.

Требуется построить оптимизационную модель рынка и рассчитать объемы спроса и предложения.

Построение модели рынка. Математическая модель рынка с четырьмя потребителями и производителями (модель 4*4) с введенными параметрами представим в виде векторной задачи линейного программирования.

opt F(X)={ max F₁(X)={max f₁(X) = 27x₁  + 50x₂, 

max f₂(X) = 26x₃+ 15x₄,

max f₃(X) = 35x₅ + 15x₆, 

max f₄(X) = 35x₇+ 28x₈}, 

min F₂(X)={min f₅(X) = 70x₁ + 55x₅ , 

min f₆(X) = 95x₂+ 35x₆,

min f₇(X) = 46x₃ + 85x₇ , 

min f₈(X) = 35x₄+ 48x₈}}, при ограничениях  8000 ≤70x₁ + 55x₅ ≤14000, 

10000 ≤ 95x₂+ 35x₆ ≤17000

9000 ≤46x₃ + 85x₇ ≤ 15500, 

12000 ≤ 35x₄+ 48x₈≤ 19000, 

43x₁+ 45x₂ ≤ 14000,            

20x₃+ 20x₄ ≤ 17000,

20x₅+ 20x₆ ≤ 15500,            

50x₇+ 20x₈ ≤ 19000,

x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈ ³ 0. 

Решение задачи в программе Scilab

disp('Исходные данные рыбной отрасли')

f=[-27 -50 0 0 0 0 0 0;

0 0 -26 -15 0 0 0 0;

0 0 0 0 -35 -15 0 0;

0 0 0 0 0 0 -35 -28;

70 0 0 0 55 0 0 0;

0 95 0 0 0 35 0 0;

0 0 46 0 0 0 85 0;

0 0 0 35 0 0 0 48]

a=[70 0 0 0 55 0 0 0;

-70 0 0 0 -55 0 0 0;

0 95 0 0 0 35 0 0;

0 -95 0 0 0 -35 0 0;

0 0 46 0 0 0 85 0;

0 0 -46 0 0 0 -85 0;

0 0 0 35 0 0 0 48;

0 0 0 -35 0 0 0 -48;

43 45 0 0 0 0 0 0;

0 0 20 20 0 0 0 0;

0 0 0 0 20 20 0 0;

0 0 0 0 0 0 50 20]

b=[14000 -8000 17000 -10000 15500 -9000 19000 -12000 14000 17000 15500 19000]

lb=[0 0 0 0 0 0 0 0]

ub=[300 300 300 300 300 300 300 300]

disp('Шаг1. Решение по каждому критерию')

[x1,f1]=karmarkar([],[],f(1,:)',[],[],[],[],[],a,b',lb',ub')

[x2,f2]=karmarkar([],[],f(2,:)',[],[],[],[],[],a,b',lb',ub')

[x3,f3]=karmarkar([],[],f(3,:)',[],[],[],[],[],a,b',lb',ub')

[x4,f4]=karmarkar([],[],f(4,:)',[],[],[],[],[],a,b',lb',ub')

[x5,f5]=karmarkar([],[],f(5,:)',[],[],[],[],[],a,b',lb',ub')

[x6,f6]=karmarkar([],[],f(6,:)',[],[],[],[],[],a,b',lb',ub')

[x7,f7]=karmarkar([],[],f(7,:)',[],[],[],[],[],a,b',lb',ub')

[x8,f8]=karmarkar([],[],f(8,:)',[],[],[],[],[],a,b',lb',ub')

disp('Шаг2. Решение (наихудшего) по каждому критерию')

[x1min,f1min]=karmarkar([],[],-1*f(1,:)',[],[],[],[],[],a,b',lb',ub')

[x2min,f2min]=karmarkar([],[],-1*f(2,:)',[],[],[],[],[],a,b',lb',ub')

[x3min,f3min]=karmarkar([],[],-1*f(3,:)',[],[],[],[],[],a,b',lb',ub')

[x4min,f4min]=karmarkar([],[],-1*f(4,:)',[],[],[],[],[],a,b',lb',ub')

[x5max,f5max]=karmarkar([],[],-1*f(5,:)',[],[],[],[],[],a,b',lb',ub')