|
||||
|
||||
 |
|
||||
|
||||
Взаимосвязь наук. Цели и задачи ТУиП
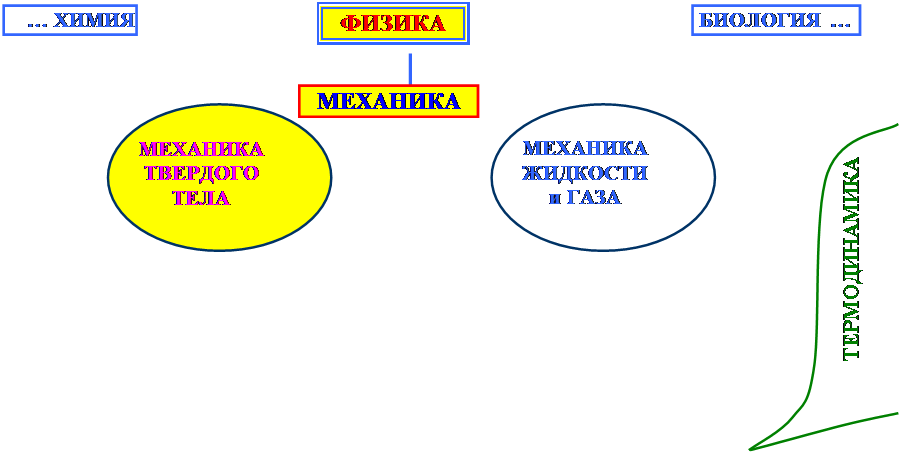
Механика как раздел физики занимает исторически центральное место среди естественных наук (химии, биологии и др.). В механике выделяют два центральных раздела:
1). механику твердого тела
2). механику жидкости и газа (гидродинамику, аэродинамику)
Механика твердого тела подразделяется на механику, изучающую
недеформируемые и деформируемые тела, с учетом свойств (идеализируемые) материала (упругие, неупругие, пластичные,
![]() вязкие и др.)
вязкие и др.)
|
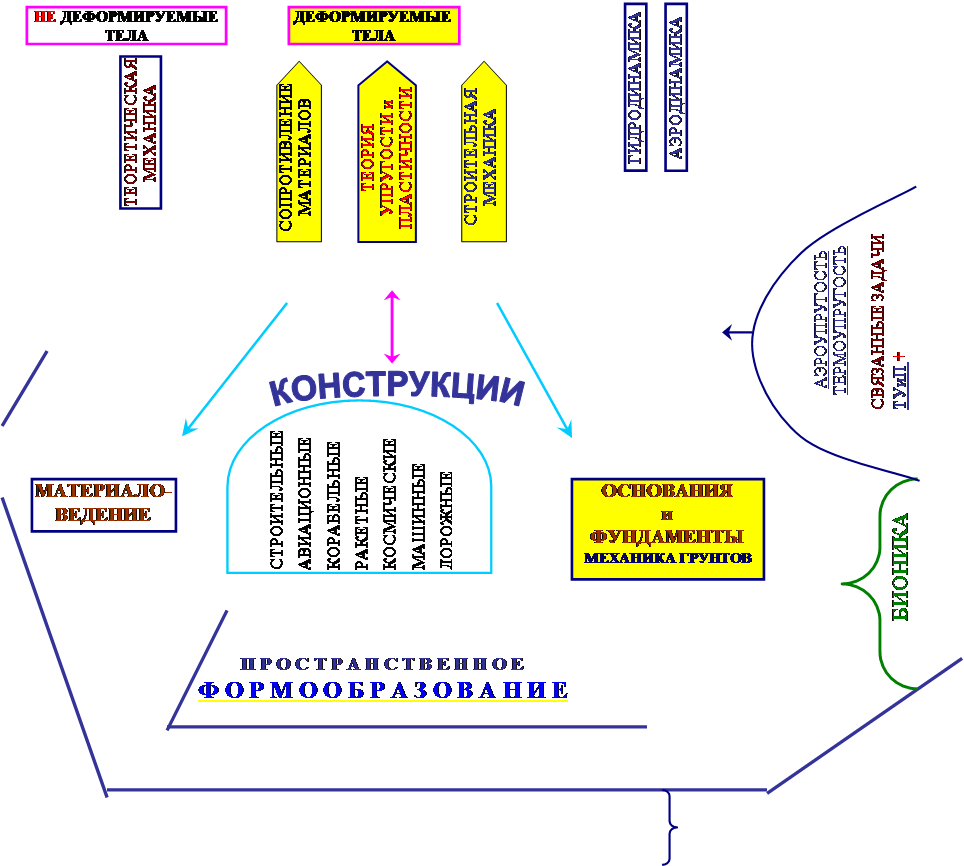
Механика деформируемого твердого тела (МДТТ) особенно важна для инженерных конструкторских задач, так как без учета деформирования нельзя решить вопросы прочности, жесткости и устойчивости конструкции. В МДТТ входят: сопр. материалов (СМ), теория упругости и пластичности (ТУиП), строительная механика систем (СМС), задачей которых является определение напряженно-деформированного состояния (НДС) отдельных тел и систем тел.
Различие между СМ и ТУиП:
СМ – изучает НДС в основном бруса, для чего принимаются упрощающие гипотезы типа плоских сечений. Это удается сделать учитывая, что два размера бруса малы по сравнению с третьим, т.е. рассматриваются в основном одномерные задачи.
ТУиП - рассматривает НДС тел любой формы и нагружения, т.е. СМ – является как бы частным случаем ТУиП.
СМС – изучает стержневые системы плоского и пространственного видов МДТТ (СМ, ТУиП, СМС) – являются фундаментальными науками для инженерных конструкций различного вида на земле, воздухе, космосе, воде, включая их взаимодействие с окружающей средой (в том числе с основанием)
В ряде случаев требуется совместный взаимосвязанный расчёт с воздействиями внешней среды, так называемые связанные задачи, в которых уравнения изменения состояния среды совместно решаются с уравнениями МДТТ (например ТУиП): задачи аэроупругости, термоупругости и др. Если же параметры состояния и воздействия внешней среды известны, то задача упрощается, т.е. например решаются уравнения ТУиП на заданные нагрузки (воздействия внешней среды) – это традиционные задачи проектирования конструкций.
Важнейшей задачей конструирования является выбор рациональной формы конструкции и оптимизация ее параметров (наука формообразования), решения которой базируются на законах ТУиП и СМС.
Рациональное конструирование базируется на знаниях и умении моделировать, т.е. представить приближенно, но достаточно точно модель реальной конструкции для расчета её НДС (выбор расчетной схемы и ее реализация, в том числе по компьютерным программам). Для моделирования используются математический аппарат (аналитический или численный, например МКЭ или МКР), а также физическое моделирование (эксперимент).
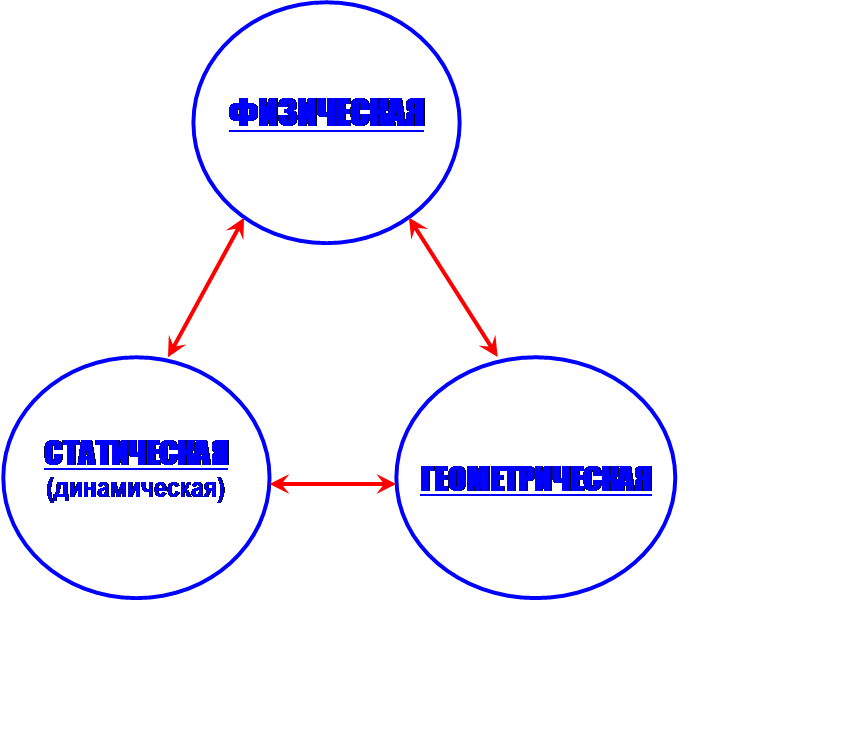
ВЗАИМОСВЯЗЬ НАУК
![]()
ЕСТЕСТВЕННЫЕ НАУКИ
 |
|||
 |
|||
![]()
![]()
|


![]() АНАЛИТИЧЕСКОЕ
АНАЛИТИЧЕСКОЕ
|
ЧИСЛЕННОЕ
|
|
Характерные отличительные задачи
|
Сопротивление материалов |
Теория упругости |
|||||||||||||||||||||
|
Гипотезы плоских сечений
|
|
|||||||||||||||||||||
 |
|
|||||||||||||||||||||
Контрольные вопросы:
1. Цель и задача ТУиП?
2. Какие тела изучает сопр. материалов, а какие ТУиП?
3. В чем принципиальное отличие теор. механики от сопротивления материалов?
4. Применимы ли гипотезы сопр. материалов (в частности, гипотезы плоских сечений) для тел любой формы?
5. Брус, балка – это трехмерные тела. На основе чего задача их деформирования сведена в сопр. материалов к одномерной задаче? (y=f1(x), s=f2(x), τ vy= f3(x) и т.д.) Можно ли подобное сделать в ТУиП?
6. Какова взаимосвязь между ТУиП и конструкциями? Почему строит. мех. и ТУиП называют фундаментальными науками?
7. Создает ли пространственное деформирование принципиальные возможности для более выгодного использования материала конструкции по сравнению с плоским или линейным (одномерным) деформированием?
|
|
|
|
|
|
|
|
|
|
|
|
|
Задачи Т.У.: определение НДСтел любой формы при любых нагрузках |
|
Контрольные вопросы:
1. В ТУиП (СМ и СМС) не рассматривается атомно-молекулярное строение тел, а принята гипотеза сплошности, следствием которой является неразрывность деформирования (т.е. после деформирования тело должно оставаться сплошным). Если после анализа результатов расчета обнаружится, что где-то нарушена неразрывность деформаций (например, два смежных сечения разошлись или повернулись на разные углы), то какой вывод Вы сделаете?
2. Представьте, что при проведенном Вами эксперименте нагружения тела обнаружится нарушение линейной зависимости между ростом нагрузки и перемещениями (деформациями), то какой вывод Вы сделаете?
3. Если при нагружении конструкции ее первоначальные размеры существенно меняются (например, размер шарика при надувании существенно увеличивается), то можно ли для определения НДС применять линейную теорию?
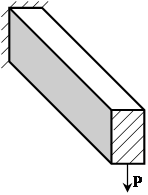
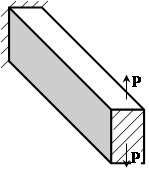
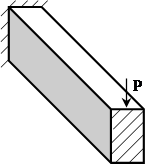
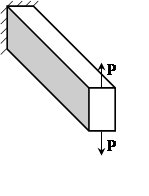
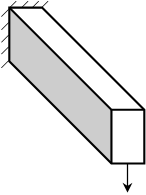
4. Покажите справедливость принципа Сен-Венана к задачам (1) и (2), используя нагружение (3). (Балка одна и таже)
|
|
|
||||||||||
 |
||||||||||||
 |
||||||||||||
 |
||||||||||||
|
|
|
|
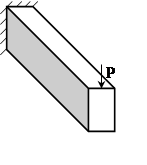 Применимы
ли эти рассуждения, т.е. справедлив ли принцип Сан-Венана, если поперечное
сечение балки в виде тонкостенного профиля?
Применимы
ли эти рассуждения, т.е. справедлив ли принцип Сан-Венана, если поперечное
сечение балки в виде тонкостенного профиля? 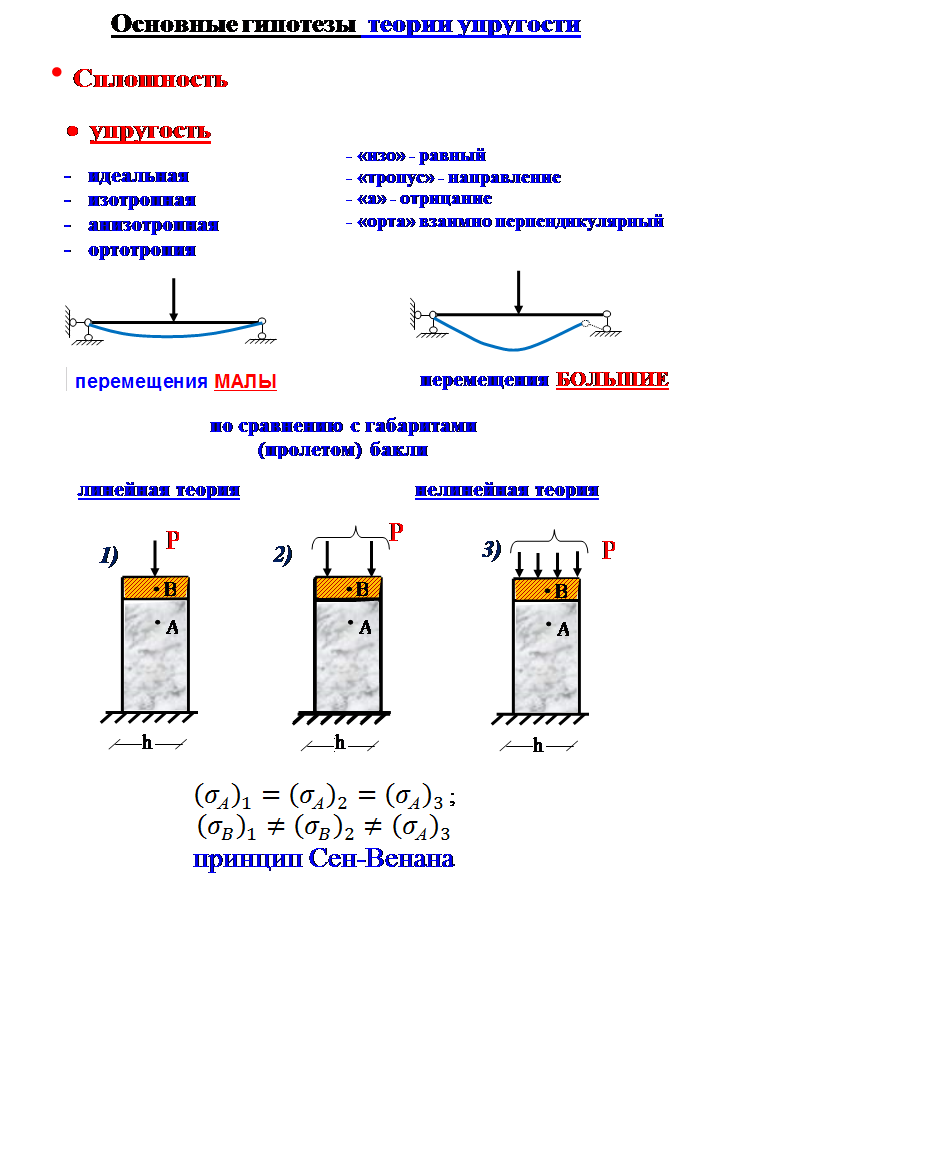 |
 |
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.