Расчеты на прочность при наличии дефектов. Дефектность материалов и конструкций. Задачи механики разрушения, страница 9

Скорость развития усталостных трещин определяется экспериментально по результатам испытаний образцов, представленных в табл. 8.2, как правило, при симметричном цикле нагружения. В процессе испытаний строится зависимость «длина трещины  - число циклов нагружения » (рис. 8.6,в), которая принимается непрерывной, и тогда скорость роста трещины определяется как касательная в точках данной зависимости

.

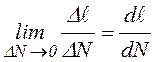В общем случае скорость развития трещины  зависит от начальной длины , уровня действующих напряжений, размеров и геометрии образцов, способа нагружения и других факторов. Прирост трещины на величину  происходит при увеличении напряжений в полуцикле растяжения. Предполагается, что при разгрузке и в полуцикле сжатия длина трещины не увеличивается. Максимальным  и минимальным  напряжениям цикла соответствуют распределения напряжений в вершине трещины, описываемые коэффициентами интенсивности напряжений. Скорость роста трещины оказывается функцией размаха коэффициента интенсивности напряжений

.   (8.23)

Диаграмма циклического разрушения (диаграмма циклической трещиностойкости) строится в логарифмических координатах в виде зависимости «» (рис. 8.6,г) и состоит из трех участков. Первый участок (I) характеризуется низкими скоростями развития трещин (10^-8 мм/цикл), второй (среднеамплитудный) участок, как правило, аппроксимируется прямой в диапазоне скоростей 10^-7 мм/цикл5×10^-3 мм/цикл, на третьем участке (III) наблюдается интенсивное увеличение скорости роста трещины (5×10^-4 мм/цикл), заканчивающееся разрушением элемента конструкции. Диаграмма последнего цикла изменения нагрузки на заключительной стадии усталостного разрушения может быть интерпретирована как диаграмма разрушения однократного нагружения (рис. 8.5). При возникновении эксплуатационных перегрузок, аварийных ситуаций разрушение элементов конструкций, имеющих усталостные трещины, может произойти на любом из трех участков диаграммы циклического разрушения с реализацией хрупкого, квазихрупкого или вязкого разрушения.

Второй участок диаграммы по данным массовых испытаний образцов для большинства конструкционных материалов описывается степенным уравнением (уравнение Пэриса, 1963 г.)

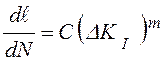,                                         (8.24)

где ,  - характеристики циклической трещиностойкости, определяемые при обработке экспериментальных диаграмм циклического разрушения.

Более полное описание диаграмм циклического разрушения дают:

уравнение Формана (1976 г.)

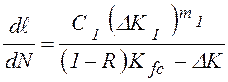;                                        (8.25)

уравнение С.Я. Яремы (1975 г.)

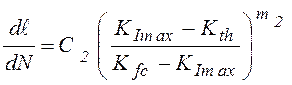,                             (8.26)

где  - коэффициент асимметрии цикла;  - критическое значение КИН в последнем цикле нагружения;  - пороговое значение размаха КИН, ниже которого не происходит развитие трещины; , , ,  - характеристики циклической трещиностойкости.

В инженерной практике наиболее часто используется уравнение Пэриса (8.24), содержащее два экспериментально определяемых параметра (, ), в отличие от уравнения Формана (три параметра - ,, ) и уравнения Яремы (четыре параметра - , , , ).

8.9. Расчеты на трещиностойкость при статическом нагружении

В механике разрушения в качестве основной расчетной характеристики используются критические коэффициенты интенсивности напряжений , которые в определенном диапазоне температур, геометрических размеров образцов и трещин имеют достаточно стабильные значения. При известных экспериментальных значениях  расчет на трещиностойкость проводится по уравнению (8.20), устанавливающему связь между разрушающими напряжениями  и размерами трещин (рис. 8.7). При напряжениях выше предела текучести уравнение (8.20) дает завышенные значения разрушающих напряжений, уровень которых в конструкционных материалах ограничивается величиной предела прочности .