Расчеты на прочность при наличии дефектов. Дефектность материалов и конструкций. Задачи механики разрушения, страница 10

Расчеты на трещиностойкость проводят на стадии проектирования и на стадии эксплуатации по результатам освидетельствования технических систем. В первом случае расчет выполняется для модельных трещин, располагаемых в наиболее опасных зонах конструкций, и проектных уровней напряжений (номинальные напряжений по брутто-сечению элемента конструкции, определенные по формулам сопротивления материалов без учета трещин). Во втором случае в расчетах используются реальные размеры и геометрия трещин и фактические эксплуатационные уровни напряжений. Определяется коэффициент интенсивности напряжений для элемента конструкции

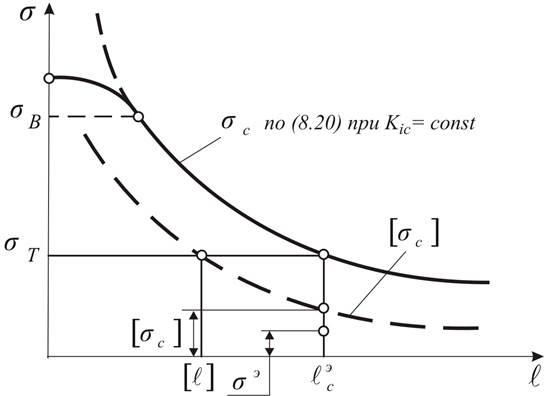
Рис. 8.7. Диаграмма разрушающих (критических) напряжений

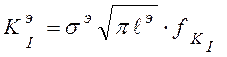,                                        (8.27)

где ,  - номинальное напряжение и размер трещины в элементе конструкции.

По аналогии с обычными условиями прочности

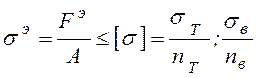
можно записать условие, ограничивающее развитие трещины

,                         (8.28)

где , ,  - коэффициенты запаса по пределу текучести, временному сопротивлению материала, по критическому коэффициенту интенсивности напряжений.

Введение коэффициента запаса  приводит к снижению диаграммы разрушающих напряжений (рис. 8.7 и 8.8). Уравнение (8.28) с использованием (8.20) можно записать в виде

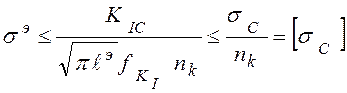.                              (8.29)

Для элементов конструкций с трещиной, наряду с , вводится запас по критическому размеру трещины

.                                             (8.30)

Это приводит к смещению диаграммы критических напряжений влево (рис. 8.8). Критический размер трещины определяется по уравнению (8.20)

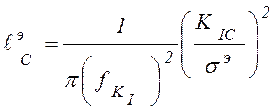.                                (8.31)

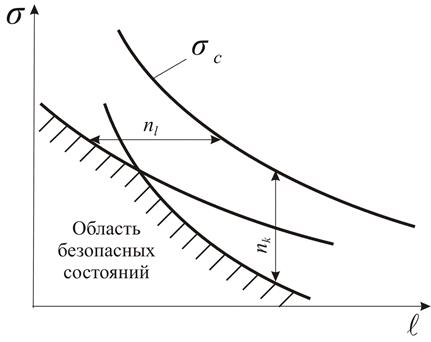
Рис. 8.8. Схема определения области безопасных состояний элементов конструкций с трещинами

Коэффициент запаса по коэффициенту интенсивности напряжений составляет 1,5…1,7, по длине трещины 2,5…5,0. Использование двух коэффициентов запаса позволяет определить область безопасных состояний элемента конструкции с трещиной, которая ограничивается нижней огибающей двух кривых (рис. 8.8).

8.10. Расчеты на трещиностойкость при циклическом нагружении

Сопротивление элементов конструкций развитию трещин при циклическом нагружении может быть оценено по кривым усталости, соответствующим различным длинам исходных трещин (рис. 8.6,а), с определением числа циклов до образования трещины  и до момента разрушения . Однако в этом случае требуется проведение большого объема модельных и натурных экспериментов.

Если при обследованиях металлоконструкций выявлены эксплуатационные трещины усталостного происхождения, то необходимо проведение расчетов на циклическую трещиностойкость. Данная задача может быть решена с использованием уравнений (2.24)-(8.26), описывающих скорость развития трещины, при известных значениях характеристик циклической трещиностойкости. В инженерной практике наибольшее распространение получило уравнение Пэриса (8.24). На первом этапе определяется размах коэффициента интенсивности напряжений для элемента конструкции

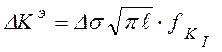, где  - длина трещины на заданной стадии нагружения;  - длина трещины в момент обнаружения;  - размах напряжений в цикле нагружения.

Подставляя выражение  в уравнение (8.24), разделяя переменные и интегрируя в пределах от  до  и от  до  (в соответствии со схемой II рис. 8.6,в) получим

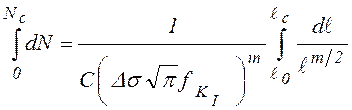.                             (8.32)

Дальнейший анализ дает следующее решение для определения критического числа циклов нагружения:

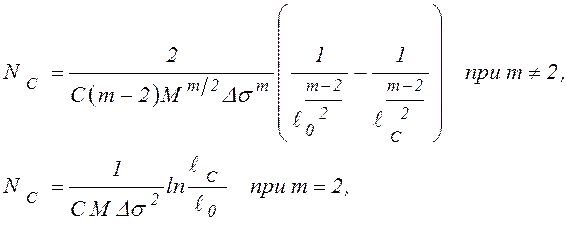              (8.33)

где .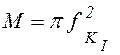

Если рассматривать промежуточные стадии развития трещин, то по уравнению (8.32) можно получить кинетическую зависимость между длиной трещины и числом циклов (рис. 8.9). Критическая длина трещины определяется по уравнению (8.31).

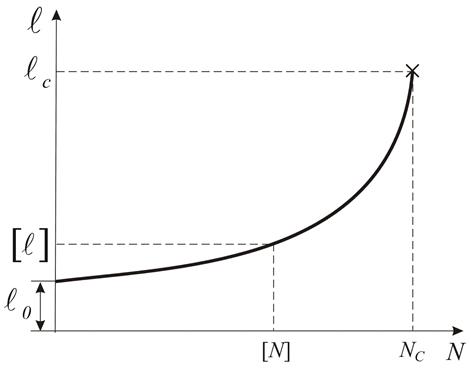
Рис. 8.9. Диаграмма разрушения при циклическом нагружении

Допустимое число циклов нагружения элемента конструкции с трещиной определяется по величине  с введением коэффициента запаса по числу циклов

.                                          (8.34)

Запасы по чиклу циклов принимаются в диапазоне 5…20.

При расследовании причин аварий и разрушений часто требуется определить исходный размер дефекта  в начальный момент эксплуатации. Для этой задачи требуется решить уравнение (8.32) относительно , при этом значение  устанавливается по поверхности разрушения, а  - по фактической истории эксплуатационного нагружения.