Расчеты на прочность при наличии дефектов. Дефектность материалов и конструкций. Задачи механики разрушения, страница 2

– проверка условий прочности ЭК с трещиной под воздействием внешней нагрузки;

– оценка величины предельной нагрузки для ЭК с трещиной;

– оценка предельного и допускаемого размеров трещины для ЭК под воздействием внешней нагрузки;

– оценка долговечности ЭК с учетом развития трещины при циклическом нагружении;

– оценка критического размера усталостной трещины для заданных уровней нагружения и сроков эксплуатации (количество циклов нагружения);

– обоснование выбора материалов с учетом сопротивления развитию трещин;

– поверочные расчеты на прочность ЭК с трещинами при проведении обследований металлоконструкций с целью определения возможностей дальнейшей эксплуатации.

8.3. Задача Гриффитса. Концепция квазихрупкого разрушения

Современные представления о процессе разрушения берут начало от работ Гриффитса (1920 – 1924 г.г.), который путем сопоставления свободной упругой энергии и поверхностной энергии тела, установил критерий разрушения для идеально-хрупкого материала. Была рассмотрена задача о растяжении плоскости с трещиной длиной , расположенной перпендикулярно направлению растяжения (рис. 8.1).

Трещина будет распространяться при напряжениях  без дополнительного подвода энергии, если уменьшение энергии упругой деформации 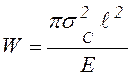 не превышает скорость увеличения поверхностной энергии , затрачиваемой на образование четырех дополнительных поверхностей трещины при плотности поверхностной энергии ,

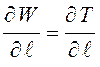.                                                   (8.1)

Лавинообразное распространение трещины произойдет в том случае, если скорость освобождения энергии упругой деформации превысит прирост поверхностной энергии трещины, т.е.:

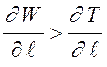.                                                  (8.2)

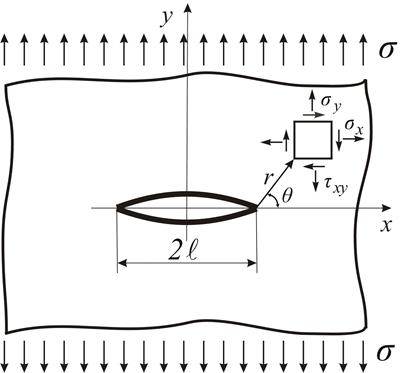
Рис. 8.1. Схема задачи Гриффитса

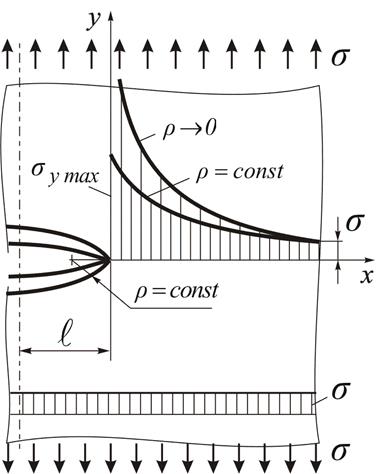
Рис. 8.2.

Распределение напряжений в пластине с эллиптическим отверстием

В соответствии с этим критическое напряжение начала распространения трещины будет:

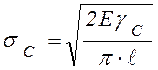.                                          (8.3)

Данный критерий справедлив для идеально упругих тел и описывает механизм хрупкого разрушения. Однако моменту, предшествующему распространению трещины, всегда сопутствует возникновение пластической области в её вершине до некоторого предельного размера, затем происходит разрушение в локальном объеме материала с последующим продвижением трещины. Учет этих особенностей привел к формулировке концепции квазихрупкого разрушения конструкционных сталей (1950-е годы, Орован, Ирвин). Энергия образования пластических деформаций  значительно превышает удельную поверхностную энергию , что позволяет произвести соответствующую замену в уравнении (8.3)

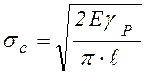.                                            (8.4)

Энергия , необходимая для продвижения трещины на единицу длины, оценивается энергией упругих деформаций, но затраты энергии на разрушение относятся к работе пластических деформаций. Предполагается, что размеры пластически деформируемых объемов значительно меньше длины трещины. Тогда условие распространения трещины для пластины единичной толщины будет:

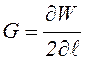,                                                   (8.5)

где  – изменение энергии упругих деформаций.

С учетом выражения для  из (8.5) получим

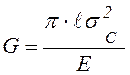.                                              (8.6)

8.4. Напряжения и деформации в вершине трещины

Работам Гриффитса предшествовали исследования Колосова Г. В., Инглиса, Мусхелишвили Н. И. (1910-1920 гг.) в результате которых была решена задача о равновесии бесконечного тела с эллиптической полостью в однородном поле напряжений  (рис. 8.2).

Наибольшие напряжения возникают в вершине отверстия на большой полуоси

,                                          (8.7)

где  – номинальные напряжения;  – теоретический коэффициент концентрации напряжений

.                                          (8.8)