Расчеты на прочность при наличии дефектов. Дефектность материалов и конструкций. Задачи механики разрушения, страница 3

В случае круглого отверстия ; . Если сохранить постоянным размер отверстия  и уменьшить радиус , то при   (рис. 8.2). В отличие от обычных форм концентрации (отверстия, выточки и т.д.) максимальные напряжения в вершине трещины при упругом деформировании оказываются неопределенными по величине (бесконечно большими) и это делает невозможным использование традиционных критериев разрушения материалов типа .

Обобщение задач о концентрации напряжений в пластинах с трещинами (Д. Ирвин, 1957-1965 гг.) позволило выделить три основных вида деформаций в вершине трещины (рис. 8.3). Общий случай деформированного состояния получается путем их наложения на основе принципа независимости действия сил. Тип I соответствует трещинам нормального отрыва, тип II - поперечному симметричному сдвигу, тип III - поперечному несимметричному сдвигу или антиплоской деформации. Для пластины, растянутой напряжениями  на бесконечности (I тип трещин) Д. Ирвин дал следующую формулу для полей напряжений (рис. 8.1):

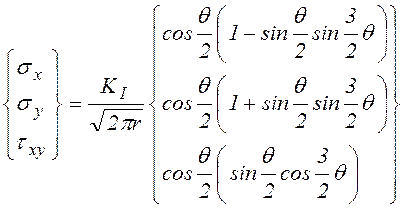,                    (8.9)

где  - коэффициент интенсивности напряжений (КИН), соответствующий I типу деформаций.

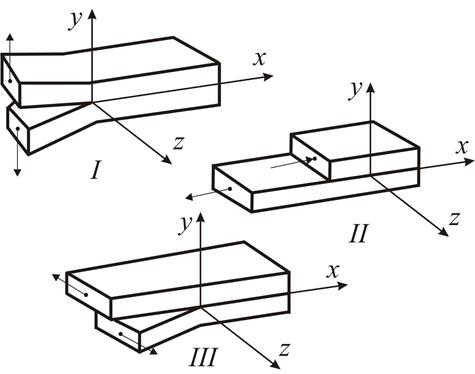
Рис. 8.3. Основные виды деформаций поверхности трещин

Каждому типу деформаций соответствуют свои коэффициенты интенсивности деформаций , ,  и функции угла . Коэффициент интенсивности напряжений в отличие от теоретического коэффициента концентрации напряжений имеет размерность ; [МПа]; [кгс×мм^-3/2].На продолжении трещины при  напряжения ,  и  будут

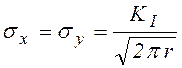;       .                           (8.10)

При известных компонентах , ,  могут быть определены главные напряжения в вершине трещин. Используя обобщенный закон Гука можно установить линейные и угловые деформации , , . Для пластины бесконечных размеров при номинальных напряжениях  (модель I) и  (модели II, III) величины коэффициентов интенсивности напряжений равны

;     ;     .                      (8.11)

Для других случаев нагружения, размеров трещин и элементов конструкций вводятся поправочные функции , , , определяемые путем решения соответствующих задач или экспериментально:

;  ;            (8.12)

Область применимости приведенных решений ограничивается уровнем номинальных напряжений (0,2...0,3). Дальнейшее повышение внешней нагрузки сопровождается значительным повышением местных напряжений, которые превышают предел текучести материала. Это является причиной образования зон пластичности в вершинах трещины, в которых наблюдается перераспределение напряжений и деформаций. Если в условие текучести Мизеса подставить величины главных напряжений, полученные на основе (8.9), то при  можно определить размер пластической зоны (модель Ирвина для трещины с зоной пластичности)

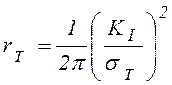.                                     (8.13)

Деформации и перемещения в пластической зоне увеличиваются, и это учитывается путем введения в уравнения (8.12) фиктивной длины трещины

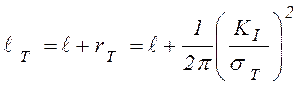.                         (8.14)

Модель трещины с пластической зоной в виде клиновидной узкой полосы была развита в работах Дагдейла, Панасюка В.В., Леонова М.Я., Уэлса (1960-1965 гг.) и послужила основой для сформулировки концепции критического раскрытия трещины. Разрушение тела с трещиной произойдет, если величина смещения противоположных берегов трещины в её вершине  при , достигнет своего критического значения . Величина раскрытия трещины определяется по формуле

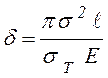.                                                  (8.15)

8.5. Критерии разрушения тел с трещинами

Анализ энергетических затрат в процессе разрушения, напряжений и деформаций в вершине трещины позволил сформулировать ряд силовых, энергетических и деформационных критериев механики разрушения. Распространение трещины возможно в случае реализации следующих условий

1. 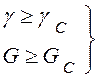    – энергетические критерии;

2. 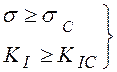    – силовые критерии;                                                  (8.16)