ГЛАВА 3. РАСТЯЖЕНИЕ И СЖАТИЕ
3.1. Основные понятия
Осевым (центральным) растяжением или сжатием называют такой вид нагружения бруса, при котором внутренние силы в поперечном сечении приводятся только к продольной силе N.
|
|
Условимся представлять брус в виде совокупности продольных элементов, параллельных оси бруса, имеющих бесконечно малые поперечные сечения. Эти элементы будем называть «волокнами».
3.1.1.
Дифференциальная зависимость между ![]() и
и ![]()
Рассмотрим стержень нагруженный продольной нагрузкой q (рис.3.2 а). Выделим из стержня элемент длиной dz (рис.3.2 б). На него будут действовать нагрузка q и продольные силы: в левом сечении – N, в правом – (N+dN), заменяющие действие отброшенных частей бруса, где dN – приращение продольной силы на участке dz.
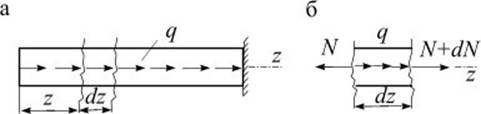
Рис. 3.2
Составим уравнение равновесия для выделенного элемента:
![]()
откуда
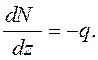 (3.1)
(3.1)
Производная от продольной силы по длине бруса равна
интенсивности распределенной нагрузкиq. По знаку производной можно судить о
росте или убывании функции. Если ![]() 0, то
продольная сила убывает. Зависимость (3.1) используется при
проверке правильности построения эпюры
0, то
продольная сила убывает. Зависимость (3.1) используется при
проверке правильности построения эпюры ![]() .
.
3.1.2. Построение эпюры продольных сил
Продольная сила Nв сечении численно равна алгебраической сумме проекций на ось Z всех внешних сил, включая и опорные реакции, действующие на отсеченную часть бруса, взятых со знаком плюс, если они направлены от сечения (растяжение), и минус – если к сечению (сжатие):
![]() (3.2)
(3.2)
Знак продольной силы ![]() определяется
по схеме: растяжение – со знаком «+» (рис. 2.2 а), сжатие – со
знаком «–» (рис. 2.2 б).
определяется
по схеме: растяжение – со знаком «+» (рис. 2.2 а), сжатие – со
знаком «–» (рис. 2.2 б).
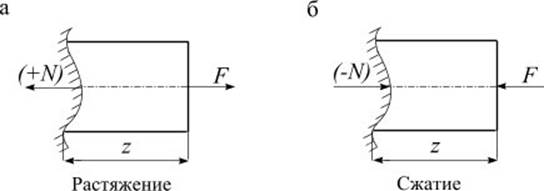
Рис. 3.3
Пример 3.1.Для бруса (рис.3.4 а) построить эпюру продольных сил N.
1. Определим реакцию заделки.
![]()
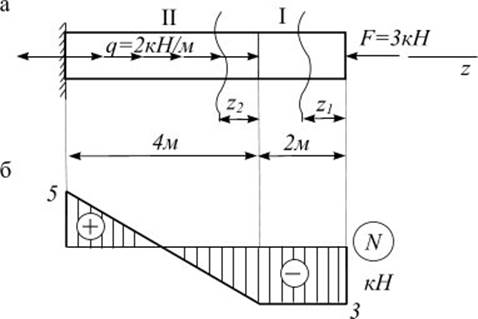
Рис. 3.4
2. Разобьем брус на два участка, и применив метод сечений, найдем продольные силы на каждом из них, рассматривая равновесие отсеченной части. Во избежании ошибки следует внутреннее усилие принимать всегда положительным.
|
![]()
![]()
На первом участке продольная сила постоянна и отрицательна.
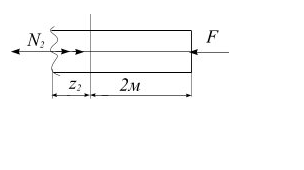 Участок II
Участок II ![]()
|
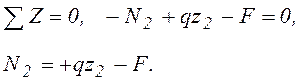
На этом участке продольная сила изменяется по линейному закону.
при ![]()
при ![]()
По найденным значениям продольных сил на отдельных участках строим эпюру N (рис.3.4 б).
1. Для бруса, закрепленного с помощью заделки, для построения эпюры, не обязательно определение опорных реакций, если оставлять часть бруса, которая не закреплена.
2. Знак усилия ![]() , получаемый из решения, позволяет
установить вид деформации – растяжение или сжатие.
, получаемый из решения, позволяет
установить вид деформации – растяжение или сжатие.
3.
Научастке
I, где ![]() ,
эпюра N – прямая, параллельная оси (
,
эпюра N – прямая, параллельная оси (![]() ).
).
4.
Научастке
II, где ![]() ,
эпюра N – наклонная прямая (N изменяется по линейному закону).
,
эпюра N – наклонная прямая (N изменяется по линейному закону).
5. В сечениях, где приложены внешние силы, внутренняя сила меняется скачкообразно, причем размер скачка равен соответствующей внешней силе. Так, скачок на уровне заделки характеризует значение реакции (Н=5 кН), скачок на свободном конце – значение внешней силы (F=3 кН).
3.2 . Напряжения в поперечных сечениях стержня
|
|
1.
|
|
2.
|
3. Физическая сторона задачи определяется законом Гука;
4. Синтез – совместное решение полученных уравнений.
Рассмотрим стержень, нагруженный силой F (рис. 3.5 а). Для произвольного сечения z (рис. 3.5 б) статическая сторона задачи выражается уравнением
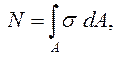 (3.3) где А – площадь поперечного сечения бруса.
(3.3) где А – площадь поперечного сечения бруса.
Рассмотрим модель стержня (рис. 3.5 в), на боковой поверхности которого нанесена ортогональная сетка из продольных и поперечных линий.
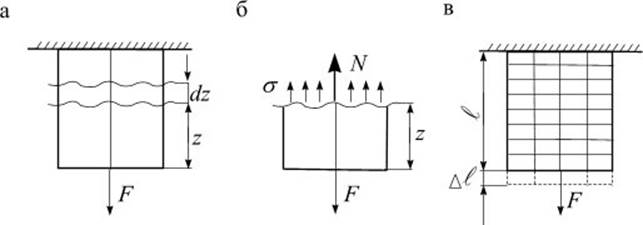
Рис. 3.5
После нагружения можно заметить, что поперечные линии смещаются вдоль продольной оси, оставаясь прямолинейными и перпендикулярными ей. Это подтверждает гипотезу плоских сечений Я. Бернулли:
сечения бруса, плоские и перпендикулярные его продольной оси до деформации, остаются плоскими и перпендикулярными оси в процессе деформации.
Продольные линии (волокна) удлиняются на одну и ту же величину
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.