Сдвиг и кручение. Чистый сдвиг. Анализ напряженного состояния при чистом сдвиге. Закон Гука при чистом сдвиге

ГЛАВА 8.СДВИГ  И  КРУЧЕНИЕ

8.1.  Чистыйсдвиг

8.1.1.  Анализ напряженного состояния при чистом сдвиге

Сдвиг – это такой случай нагружения, когда в поперечном сечении возникает только поперечная сила .

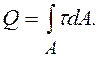                                                     (8.1)

Однородный чистый сдвиг можно получить нагружением пластины, захваченной в жесткие контурные шарнирно соединенные накладки (рис.8.1 а).

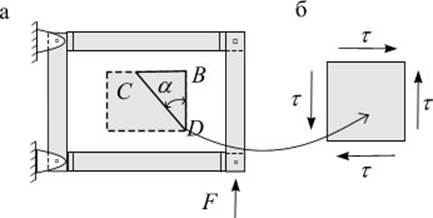
Рис. 8.1

Для всех точек пластины касательные напряжения  будут равны

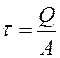,                                                      (8.2)

где  – сдвигающая сила;  – площадь сечения пластины; а касательные напряжения  принимаем равномерно распределенными по сечению. На гранях выделенного прямоугольного элемента возникают только касательные напряжения (рис. 8.1 б).

Такое напряженное состояние называется чистым сдвигом.

Посмотрим, как при чистом сдвиге изменяются напряжения в зависимости от ориентации секущих площадок. Выделим трехгранную призму DCB (рис.8.1) и рассмотрим ее в равновесии (рис. 8.2).

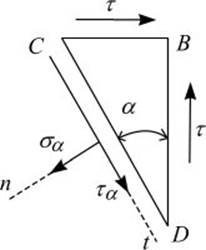
Рис. 8.2

На грани DС возникают как касательные, так и нормальные напряжения. Проецируем все силы, действующие на элемент, на оси n и t.

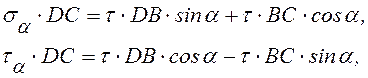
где  и , получаем

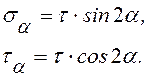                                                (8.3)

При = 0 и = 90⁰ напряжения = 0, =t. При = ± 45⁰ напряжения = 0, = ±t. Следовательно, на гранях элемента, повернутого на 45⁰, будут обнаружены только нормальные напряжения, причем на одной паре граней они растягивающие, на другой - сжимающие (рис. 8.3).

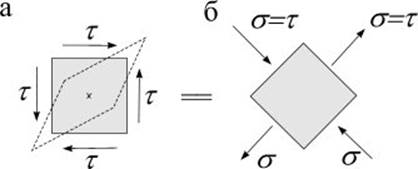
Рис. 8.3

Чистый сдвиг может быть представлен как одновременное растяжение и сжатие по двум взаимно перпендикулярным направлениям.

8.1.2.  Закон Гука при чистом сдвиге

τ

Рассмотрим деформацию элемента со стороной а, закрепив одну грань (рис. 8.4).

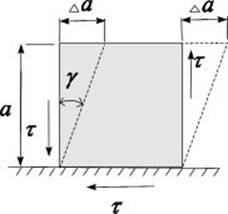
Рис. 8.4

Малый угол , на который изменяется первоначально прямой угол, называется углом сдвигаилиотносительным сдвигом. Величину абсолютного смещения грани  называют абсолютным сдвигом.

Учитывая малость , можно записать:

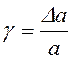  или  .                                       (8.4)

Деформация сдвига характеризуется изменением углов элемента, длина ребер не меняется (рис. 8.3 а).

Из опытов на кручение трубчатых образцов из пластичной стали получают диаграмму сдвига в координатах  (рис. 8.5). В пределах упругих деформаций справедлива линейная зависимость: закона Гука при сдвиге

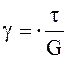 ,   или  ,                                        (8.5)

где  – модуль упругости материала при сдвиге (Па). Для стали = 8×10⁴МПа.

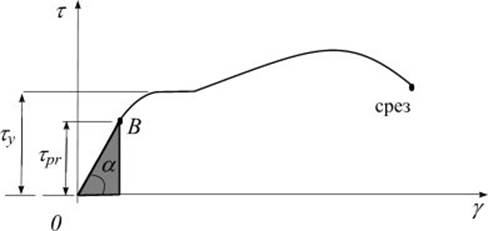
Рис. 8.5

Для изотропного материала между ,  и , характеризующими упругие свойства, существует зависимость

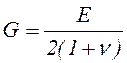.                                                  (8.6)

Перепишем (8.4) с учетом (8.5) и  (8.2), получим закон Гука для абсолютного сдвига:

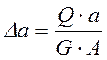,                                                (8.7)

где  – жесткость бруса при сдвиге.

8.1.3.  Потенциальная энергия при чистом сдвиге

Потенциальная энергия деформации рассматриваемого элемента равна работе касательных (сдвигающих) сил, приложенных к граням элемента:

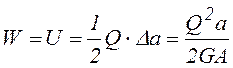.                                       (8.8)

Объем элемента V, поэтому удельная потенциальная энергия:

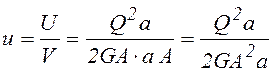, или с учетом (8.2)

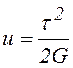,                                                      (8.9)

причем численно она равна площади треугольника на диаграмме сдвига (рис.8.5).

8.1.4.  Понятие о срезе и смятии

Срезом называют такой вид нагружения бруса, при котором в поперечном сечении возникает только поперечная сила Q.

Деформация среза имеет место при действии на брус с противоположных сторон двух равных сил на близком расстоянии друг от друга (рис. 8.6  а).

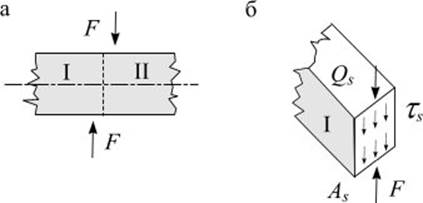
Рис. 8.6

Примером такого действия сил на брус может быть разрезание ножницами прутьев, полосы и т.п.

Рассмотрим отсеченную часть I в равновесии (рис. 8.6 б), очевидно

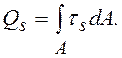                                                (8.10)

Принимая  равномерно распределенными по площади сечения , будем иметь , и условие прочности на срез принимает вид

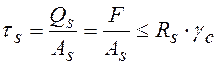,                                         (8.11)

где  – срезающая сила;  – площадь среза;  – расчетное сопротивление материала срезу.

Расчет на срез во многих случаях сопровождается расчетом на смятие.

Смятие - это пластическая деформация, возникающая на поверхностях контакта.

Условие прочности на смятие:

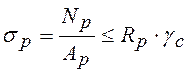  ,                                           (8.12)

где – расчетная сила смятия; – площадь смятия; – расчетное