зависимости от условий нагружения и испытаний один и тот же материал может находиться в различных механических состояниях: упругом, упруго-пластическом, пластическом и в состоянии разрушения. Предельное состояние материала как состояние разрушения может реализоваться как в пластичных материалах, так и в хрупких. Для пластичных материалов характерна следующая последовательность смены механических состояний:
- упругая стадия деформирования;
- пластическая стадия (накопление повреждений, пластическое течение);
- стадия разрушения (накопление повреждений и образование микротрещин; развитие магистральной трещины до разрушения по механизму среза).
Для материалов, находящихся в хрупких состояниях, вторая стадия исключается, т.к. пластические деформации ограничены по величине и существенно локализованы, а разрушение происходит хрупко после развития магистральной трещины по механизму отрыва.
Переход материала от упругой стадии деформирования к пластической описывается критериями пластичности, а от упругого деформирования к разрушению - критериями разрушения.
10.2. Понятие о предельном состоянии материала
В общем случае
при объемном н. с. (![]() ) опасное
предельное состояние металла возникает, когда некоторая функция главных
напряжений
) опасное
предельное состояние металла возникает, когда некоторая функция главных
напряжений ![]() достигнет своего предельного
значения:
достигнет своего предельного
значения:
![]() ,
(10.1)
,
(10.1)
где ![]() -
критерий предельного состояния.
-
критерий предельного состояния.
Уравнение (10.1) в зависимости от природы материала (пластичный, хрупкий) характеризует:
-
начало
пластического течения, тогда ![]() является критерием
пластичности (текучести);
является критерием
пластичности (текучести);
-
момент
разрушения и ![]() являются критерием
разрушения.
являются критерием
разрушения.
Если выполняется условие
![]() ,
(10.2)
,
(10.2)
то материал, согласно критерию пластичности, не переходит в пластическое состояние, сохраняя упругие свойства, а, согласно критерию разрушения, в материале не образуется трещин, приводящих к разрушению.
Условие (10.1)
геометрически интерпретируется в трехмерном пространстве ![]() поверхностью, ограничивающей
область безопасных напряженных состояний, с точки зрения наступления текучести
или разрушения.
поверхностью, ограничивающей
область безопасных напряженных состояний, с точки зрения наступления текучести
или разрушения.
10.3. Критерии пластичности
10.3.1. Критерий наибольших касательных напряжений.
III теория прочности
Пластическая деформация обусловлена сдвигами кристаллической решетки металла, приводящими к возникновению плоскостей скольжения – линии Людерса – Чернова.
Предполагается,
что критерий наступления пластического состояния связан с достижением некоторой
функцией ![]() величины наибольшего
касательного напряжения
величины наибольшего
касательного напряжения ![]() , т.е.
, т.е.
![]() .
(10.3)
.
(10.3)
При объемном напряженном состоянии:
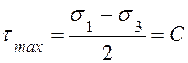 .
(10.4)
.
(10.4)
С другой стороны, в условиях одноосного растяжения, при которых проводятся испытания по определению механических свойств материалов, предельное состояние наступления пластических деформаций опишется соотношением:
![]() ;
;
![]() ; тогда
; тогда ![]() , (10.5)
, (10.5)
где ![]() –
предел текучести при одноосном растяжении.
–
предел текучести при одноосном растяжении.
Сопоставляя (10.4) и (10.5), получим условие пластичности в виде
![]()
![]() . (10.6)
. (10.6)
Критерий наибольших касательных напряжений был предложен Ш. Кулоном (1773 г.), а в качестве условия пластичности Г. Треска (1868 г.) и впоследствии математически обоснован Сен-Венаном.
Условие (10.6) не
учитывает влияние среднего напряжения ![]() на
наступление пластического состояния, однако эксперименты Лоде (1926
г.) показали, что это влияние необходимо учитывать.
на
наступление пластического состояния, однако эксперименты Лоде (1926
г.) показали, что это влияние необходимо учитывать.
10.3.2. Энергетическийкритерий.
Критерий наибольших октаэдрических касательных напряжений.
IV теория прочности
Губер (1904
г.) и Генки (1924 г.) предположили, что критерий достижения пластического
состояния должен быть связан с накопленной в единице объема удельной
потенциальной энергией деформации (ПЭД), а именно с той ее частью, которая
связана с энергией формоизменения ![]() . Была
исключена из рассмотрения энергия изменения объема
. Была
исключена из рассмотрения энергия изменения объема ![]() ,
т.к. при всестороннем сжатии
,
т.к. при всестороннем сжатии ![]() пластические
деформации не возникают, а ПЭД возрастает. Итак, когда энергия формоизменения
пластические
деформации не возникают, а ПЭД возрастает. Итак, когда энергия формоизменения ![]() , соответствующая некоторой функции
, соответствующая некоторой функции
![]() , достигнет предельного
значения, наступает состояние текучести, т. е.
, достигнет предельного
значения, наступает состояние текучести, т. е.
![]() .
(10.7)
.
(10.7)
При объёмном напряженном состоянии:
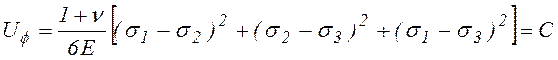 .
(10.8)
.
(10.8)
При чистом сдвиге
![]() , и изменение ПЭД
происходит только за счет энергии формоизменения
, и изменение ПЭД
происходит только за счет энергии формоизменения ![]() .
.
При одноосном растяжении предельное состояние описывается соотношениями:
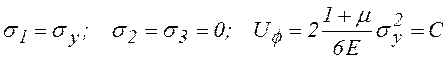 . (10.9)
. (10.9)
Тогда условие пластичности будет в виде
![]()
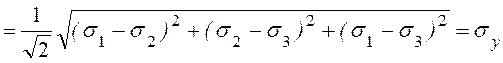 . (10.10)
. (10.10)
Выражение для энергии формоизменения (10.8) с точностью до постоянного множителя совпадает с выражением для касательного октаэдрического напряжения:
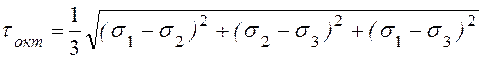 , (10.11)
, (10.11)
т. е.
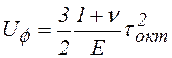 .
(10.12)
.
(10.12)
Поэтому Р. Мизес
(1913 г.) в качестве критерия предельного состояния при наступлении условий
текучести принял величину касательного напряжения на октаэдрической площадке ![]() и с учетом того, что при осевом
растяжении в предельном состоянии (
и с учетом того, что при осевом
растяжении в предельном состоянии (![]() ,
, ![]() ):
):
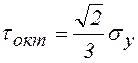
получил аналогичное условие пластичности в форме уравнения (10.10).
В условиях
чистого сдвига (![]() ,
, ![]() ,
, ![]() )
теория Треска–Сен–Венана (10.6) дает:
)
теория Треска–Сен–Венана (10.6) дает:
![]() ,
(10.13)
,
(10.13)
а теория Губера – Мизеса (10.9):
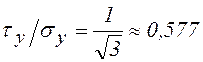 .
(10.14)
.
(10.14)
Для большинства конструкционных металлов соотношение (10.14) согласуется с результатами экспериментов лучше, чем (10.13). Наибольшее расхождение имеет место при чистом сдвиге – 15 %. Однако обе теории пластичности получили широкое распространение в практических расчетах.
10.4. Критерии разрушения
10.4.1. Критерий максимальных нормальных напряжений.
I теория прочности
Предельное состояние разрушения естественно связать с максимальным нормальным напряжением, т. е.
![]() .
(10.15)
.
(10.15)
Согласно (10.15),
разрушение произойдет в той точке тела, где величина ![]() достигнет
достигнет
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.