Геометрические характеристики плоских сечений. Статические моменты площади. Центр тяжести площади. Моменты инерции сечений

ГЛАВА 6.ГЕОМЕТРИЧЕСКИЕ  ХАРАКТЕРИСТИКИ

  ПЛОСКИХ СЕЧЕНИЙ

6.1.  Статические моменты площади. Центр тяжести площади

Рассмотрим произвольную фигуру (поперечное сечение бруса), связанную с координатными осями Оx и Оy (рис. 6.1).

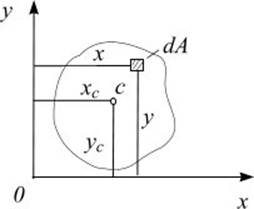
Рис.6.1

Выделим элемент площади dA с координатами х, у. Площадь сечения равна сумме элементарных площадок   

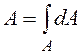.                                                                  (6.1)

Статическим моментом сечения относительно данной оси называется взятая по всей его площади A cумма (интеграл) произведений элементарных площадок dA на их расстояния до этой оси.

Так статические моменты площади сечения относительно осей x и y определяются по формулам:

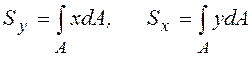.                                    (6.2)

Статические моменты измеряются в единицах длины в кубе и выражаются в см³, м³. В зависимости от знаков координат они могут принимать положительные значения, отрицательные и равные нулю.

Пусть x_c и y_c – координаты центра тяжести фигуры (рис.6.1). На основании теоремы Вариньона (из курса теоретической механики) можно записать:

,   ,                                         (6.3)

где А- площадь фигуры.

Оси, проходящие через центр тяжести называется центральными. В этом случае

, тогда . Следовательно,  статические моменты относительно центральных осей равны нулю.

Если сечение можно разбить на простейшие составные части (прямоугольники, прямоугольники и т.п.), площади и положение центров тяжести которых известны, то статический момент площади всего сечения относительно любой оси (рис. 6.2) равен алгебраической сумме статических моментов составляющих фигур относительно той же оси:

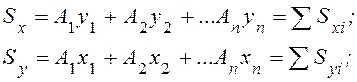                            (6.4)

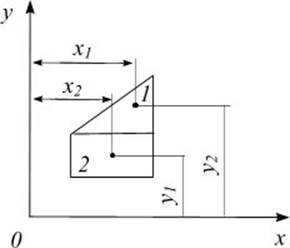
Рис.6.2

По формулам (6.3) и (6.4) легко найти координаты центра тяжести сложной фигуры:

(6.5)

,

.

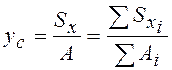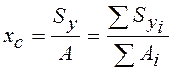Для симметричных сечений определение положения центра тяжести значительно упрощается. При наличии двух или более осей симметрии (прямоугольник, двутавр, круг и т.д.) центром тяжести является точка пересечения этих осей. Если сечение имеет одну ось симметрии (швеллер, равнополочный уголок и т.д.), то для определения положения центра тяжести необходимо найти только одну координату – вдоль оси симметрии.

Пример 6.1. Определить положение центра  тяжести сечения (рис.6.3)

Решение. Сечение симметрично относительно оси у . Следовательно, центр тяжести С лежит на этой оси, т.е. координата х_с=0, и остается найти координату у_с. Все размеры показаны на рисунке в сантиметрах.

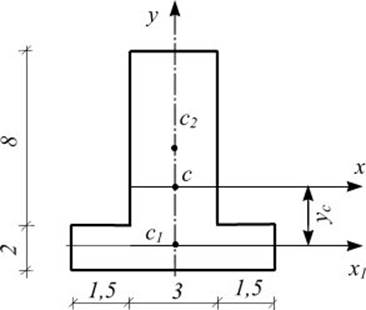
Рис.6.3

Разбиваем фигуру на два прямоугольника: первый – с центром тяжести С₁ и площадью

Второй – с центром тяжести С₂ и площадью

За вспомогательную ось принимаем центральную ось первого прямоугольника х₁. Тогда статический момент его площади . Статический момент площади второго прямоугольника согласно формулам (6.3) составляет

.

Координата центра тяжести всего сечения согласно формулам (6.5):

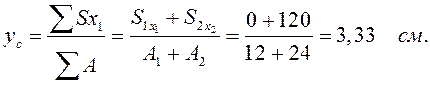
Положительное значение свидетельствует о том, что центр тяжести С лежит выше оси х₁.

Примечание. Заметим, что точка С лежит на прямой С₁С₂ соединяющей центры тяжести прямоугольников, и разбивает ее на отрезки обратно пропорциональные площадям:

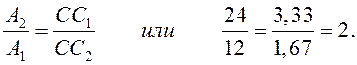
6.2.  Моменты инерции сечений

Осевым моментом инерции сечения относительно данной оси называется взятая по всей его площади A сумма произведений элементарных площадок dA на квадраты их расстояний до этой оси.

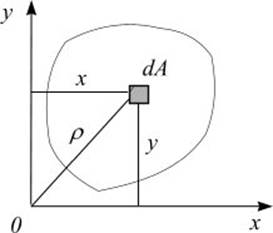
Рис.6.4

Так осевые моменты инерции относительно осей х и у равны (рис.6.4).

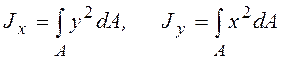.                                    (6.6)

Пусть r – расстояние элементарной площади до точки О (рис. 6.4).

Полярным моментом инерции сечения относительно некоторой точки (полюса) называется взятая по всей его площади A сумма произведений элементарных площадок dA на квадраты их расстояний r до этой точки. Следовательно

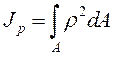.                                                 (6.7)

Как видно из рис. (6.4): , тогда

Следовательно,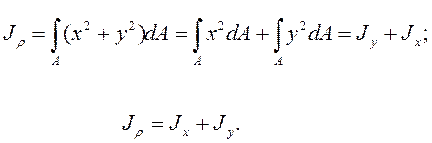                         (6.8)

Полярный момент инерции  равен сумме осевых моментов инерции J и J, взятых относительно любой пары взаимно перпендикулярных осей x и y, проходящих через полюс О.

Отметим, что осевые и полярные моменты инерции всегда положительны.

Центробежным моментом инерции сечения относительно осей координат x и y называется взятая по всей его площади A сумма произведений элементарных площадок dA на их расстояния до этих осей:

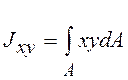.                                                  (6.9)

Моменты инерции выражаются в см⁴, м⁴ и т.д.

В зависимости от положения осей центробежный момент инерции может быть положительным, отрицательным или равным нулю. Так, например, центробежный момент сечения, показано