проектировании и расчетах на прочность и жесткость необходимо знать свойства материалов, сведения о которых можно получить путем механических испытаний на растяжение, сжатие, сдвиг, кручение и изгиб.
Наиболее распространенным является испытание на растяжение образцов специальной формы – цилиндрических или плоских (рис. 4.1 а б).
Различают длинные образцы с отношением ![]() = 10 и короткие с
= 10 и короткие с ![]() = 5, где
= 5, где ![]() –
рабочая часть образца. Согласно принципу Сен–Венана, напряженное состояние на
этом участке не зависит от способа приложения нагрузки к образцу и может
считаться однородным.
–
рабочая часть образца. Согласно принципу Сен–Венана, напряженное состояние на
этом участке не зависит от способа приложения нагрузки к образцу и может
считаться однородным.
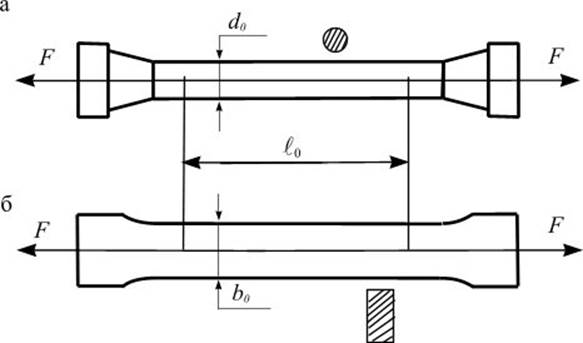
Рис. 4.1
Испытание на растяжение проводят на специальных разрывных или
универсальных машинах, создающих постепенно возрастающую нагрузку на образец.
Машины снабжены устройством для автоматической записи диаграммы растяжений,
т.е. графика зависимости между растягивающей силой ![]() и
удлинением образца
и
удлинением образца ![]() .
.
4.3. Диаграмма растяжения низкоуглеродистой стали
4.3.1. Определение характеристик прочности
На рис. 4.2 изображена диаграмма растяжения строительной стали марки Ст 3 с содержанием углерода не более 0,22 %. Рассмотрим характерные участки и точки этой диаграммы, а также соответствующие им стадии деформирования образца.
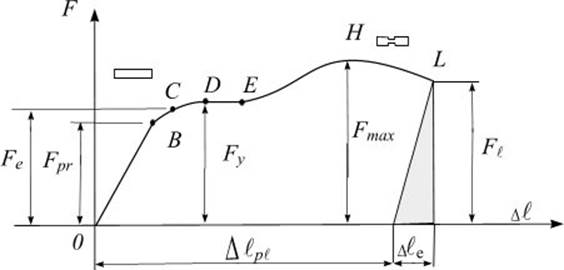
Рис. 4.2
Участок ОВ – зона пропорциональности. Зависимость между удлинением образца
и силой носит линейный характер, что подтверждает справедливость закона Гука. Эта
зависимость сохраняется до силы ![]() (точка В
на диаграмме ), которая используется для определения предела пропорциональности:
(точка В
на диаграмме ), которая используется для определения предела пропорциональности:
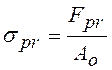 ,
(4.1)
,
(4.1)
где ![]() – начальная площадь сечения
образца. Для Ст. 3
– начальная площадь сечения
образца. Для Ст. 3 ![]() = 195 ... 200 МПа.
= 195 ... 200 МПа.
Пределом пропорциональности называется наибольшее напряжение, до которого сохраняется закон Гука.
Если по достижении точки В сбросить нагрузку до нуля,
то график разгрузки совпадет с графиком нагружения. Это говорит о том, что при
напряжениях ![]() возникают только упругие
деформации.
возникают только упругие
деформации.
УчастокОС – зона упругости. Выше точки В диаграмма искривляется, закон Гука нарушается,
деформации начинают расти быстрее роста напряжений. На этом участке в
непосредственной близости от точки В находится точка С, соответствующая
пределу упругости ![]() (индекс «е» –
упругий, от англ. elastic):
(индекс «е» –
упругий, от англ. elastic):
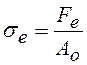 .
(4.2)
.
(4.2)
Пределом упругости называется наибольшее напряжение, до которого остаточная деформация при разгрузке не обнаруживается.
Как уже указывалось, остаточная деформация не исчезает после удаления нагрузки.
Для Ст 3 ![]() = 205 ... 210 МПа,
т.е.
= 205 ... 210 МПа,
т.е. ![]() и
и ![]() незначительно
отличаются, и обычно считают, что они практически совпадают.
незначительно
отличаются, и обычно считают, что они практически совпадают.
УчастокDЕ - площадка текучести. После точки С диаграмма искривляется
и переходит в почти горизонтальный участок. Здесь материал как бы уподобляется
жидкости и течет. Стрелка силоизмерительного механизма на время
останавливается, т.е. образец удлиняется при фактически постоянной нагрузке
равной ![]() (у – текучесть, от англ.yield). Соответствующее напряжение
вычисляется по формуле:
(у – текучесть, от англ.yield). Соответствующее напряжение
вычисляется по формуле:
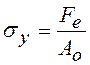 .
(4.3)
.
(4.3)
Пределом текучести называется напряжение, при котором образец деформируется без заметного увеличения нагрузки.
Для Ст 3 ![]() = 220 ... 250 МПа.
= 220 ... 250 МПа.
На полированном образце появляется сетка полос, наклоненных к оси образца под углом 450, называемых линиями Людерса-Чернова (рис. 4.3).
![]()
Рис. 4.3
Эти полосы представляют собой микроскопические неровности, возникающие вследствие необратимых сдвигов, происходящих в кристаллах под действием наибольших касательных напряжений. Описанные явления вызывают изменение внутренней структуры металла, что приводит к его упрочнению.
УчастокЕН–
зона упрочнения. Диаграмма после зоны текучести снова становится криволинейной. Образец
приобретает способность воспринимать возрастающие усилия до значения ![]() (точка Н на диаграмме),
которое используется для определения временного сопротивления или
условного предела прочности
(точка Н на диаграмме),
которое используется для определения временного сопротивления или
условного предела прочности![]() (и –
предельное значение, от англ. ultimate):
(и –
предельное значение, от англ. ultimate):
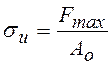 .
(4.4)
.
(4.4)
Временным сопротивлением (условным пределом прочности) называется напряжение, соответствующее наибольшей нагрузке, предшествующей разрушению образца.
Для Ст 3 ![]() = 370 ... 470 МПа.
= 370 ... 470 МПа.
УчастокHL – зона местной текучести.
После достижения усилия ![]() удлинение образца происходит на небольшом
удлинение образца происходит на небольшом
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.