Основные сведения о грунтах. Терминология, классификация, оценочные критерии свойств и характеристик, пригодность в инженерно-строительной деятельности, страница 8

Перечисленные зависимости являются важнейшими закономерностями, которыми описываются механические свойства грунтов – они создают (совместно с уравнениями механики дисперсных сред) систему, достаточную для решения инженерных задач, что иллюстрируется  табл.8.

Таблица 8

Свойство	Закономерность	Показатель	Практическое приложение
Сжимаемость	Закон уплотнения	Коэффициент уплотнения- m0	Расчет осадок во времени
Водопроницаемость	Закон ламинарной фильтрации v = кф i	Коэффициент фильтрации- кф	Прогноз скорости осадки водонасыщенных грунтовых оснований
Контактная сопротивляемость сдвигу	Предельное сопротивление сдвигу – tu. Условие  прочности tu= ptgj + c	Коэффициент внутреннего трения и сцепления - j и с	Расчеты прочности, устойчивости и давления на ограждения
Структурно-фазовая деформируемость	Принцип линейной деформируемости	Модуль деформации – Е0	Определение деформаций грунтов, расчет осадок оснований

2.3 Напряжения в грунтах

Возникающие в грунтах деформации являются следствием действующих напряжений; как и в твердом теле, напряжение создается в любой точке основания и характеризуется шестью компонентами: нормальными - s_z, s_x, s_y, s_xy, касательными -t_хy,t_zx, t_zy и тремя главными напряжениями s₁, s₂ и s_3.

Различают виды задач теории напряжений: пространственная, плоская и линейная, принятая в механике грунтов система координат и компоненты напряжений показаны на рис.5.

 

 

 

22

Рис.5. Схема напряжений в элементе грунта:

при равномерной нагрузке (плоская задача)

t_ZX, t_ZY и t_XY  - касательные напряжения

 (на рисунке не показаны)

Напряжение в грунте от собственного веса определяется по формуле ;

если слои имеют разное значение удельного веса то

.

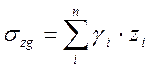Если в грунте находится горизонт подземных вод - WL, нижележащие (дренирующие) грунты взвешиваются, и значение удельного веса принимается, равным g_sb; эпюры напряжений приведены на рис.6.

Рис.6. Характерные эпюры распределения напряжений

от собственного веса грунта

23

Напряжения в грунте в точках по оси z при равномерной нагрузке на поверхности определяются по формуле

, где a - коэффициент рассеивания, принимаемый для пространственной задачи в зависимости от  (l- длина, b – ширина подошвы фундамента) и для плоской задачи при 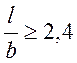  по табл.7.

Напряженное состояние в грунте иллюстрируется эпюрами и изобарами; изобары – линии, соединяющие точки с одинаковыми напряжениями s_zp.

Примеры эпюр для s_zp и изобар для напряжений s_zp, s_хp, s_чz даны на рис. 7.-9.

Рис. 7.  Эпюры распределения сжимающих напряжений s_z :

 а - по вертикальным сечениям массива грунта; б – по горизонтальным сечениям массива грунта.

Рис. 8. Характер распределения напряжений s_z  по оси фундамента

 в зависимости от формы и площади его подошвы:

1 – для квадратного фундамента; 2 – для ленточного фундамента шириной b=1 м; 3 – для ленточного фундамента ширинойb=2 м

24

Рис. 9. Линии равных напряжений

 в линейно деформируемом массиве

при плоской задаче:

а – для s_z (изобары); б – для s_х (распор); в – для t (сдвиг)

Главные напряжения s₁ и s₂ (рис. 10.) для плоской задачи направлены по биссектрисе угла видимости a и находятся по формулам

,  .

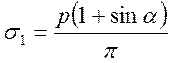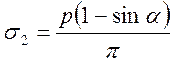В точках, лежащих на оси Z , соблюдается условие t_zx=0, s_zр=s₁.

Рис. 10.  Схема действия главных напряжений в условиях плоской задачи

25

2.4 Контактные напряжения

Так называются напряжения s_zр, возникающие непосредственно под подошвой фундамента на контакте с грунтом. Они зависят от жесткости фундамента. Поскольку предпочтение в проектной практике отдается жестким или условно жестким фундаментам, то при центральном загружении эпюра контактных напряжений имеет вид прямоугольника; при внецентренном загружении – трапеции, при этом в первом случае 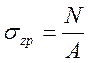; во втором 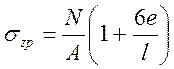, где е – эксцентриситет, равный .