Рассмотрим уравнение равновесия частицы грунта М на откосе с углом естественного откоса - a и углом j (внутреннего трения) для грунта слагающих откос (рис. 2.12).
Рис. 12.
Раскладывая силу F на составляющие N и T, имеем:
N = Fcosa
Tu = Fsina
Удерживает частицу на откосе сила трения T = Ntgj или T = Fcosatgj.
Условие равновесия имеет вид
Т = Tu
F cosa tgj = F sin a или tgj = tga.
j = a
Это условие равновесия песчаного откоса. Откос будет устойчивым, если j > a на величину коэффициента надежности gn (коэффициент запаса устойчивости). В соответствии с нормами его значение принимают gn= 1,05…1,35, в зависимос-
29
ти от уровня ответственности сооружения.
Устойчивость откоса, сложенного глинистым грунтом, определяется в предположении, что при обрушении откоса образуется круглоцилиндрическая поверхность скольжения, как это показано на рис.13.
рис.13.
Вычислим равновесие выделенного отсека:
Ni = Fi cosai, Ti = Fi sinai
где Fi – вес отсека, Ni - нормальная составляющие силы Fi; Ti - касательная составляющие силы Fi.
Удерживающая сила трения Tfi = Nitgj = Fi cosai tgjи сцепление
сi = cDli , где Dli –длина дуги отсека.
Предельное состояние возникает при равенстве удерживающих и сдвигающих сил. Для отсека выражение устойчивости запишется в виде
Fi cosai tg j+сDl= Fi sinj.
Для всего откоса
справедливо равенство моментов сил, удерживающих и сдвигающих отсеки
относительно точки центра вращения О. Таким образом, Муд =
R(SFi cosai tgj +сL), а момент сдвигающий Мсд
= RSFisinai. Коэффициент надежности (устойчивости)
откоса равен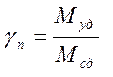 
, его принимают
в пределах 1,05…1,5. В итоге получаем
.
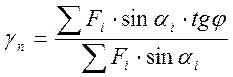Задача осложняется тем, что положение центра О не определено. Существуют разные способы его определения. В расчетах рекомендуется использовать решение этой задачи М.Н.Гольдштейном по предложенной формуле
30
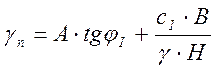, где А и В -
коэффициенты, принимаемые по графику в зависимости от высоты - Н, заложения откоса m и глубины (ниже подошвы откоса)
наиболее опасной кривой скольжения.
Более подробно метод изложен в примере решения задачи – там же даются таблица коэффициентов А и В и необходимые пояснения. Высота откоса Н с заданным значением коэффициента надежности может быть найдена по формуле
.
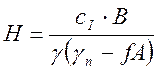2.8 Определение давления грунта на ограждения в виде подпорных стен, стен подвалов и подземных сооружений, устьев мостов и набережных
Различают несколько видов задач по определению активного (стенка движется от грунта) и пассивного (при навале стенки на грунт) давления грунта на ограждения.
Задача 1. Грунт за стенкой сыпучий, стенка гладкая, вертикальная (рис.14).
Рис.14. Схема действия сил и эпюры давления сыпучего грунта для гладкой стенки:
а - при действии равномерно распределенной нагрузки; б – при действии собственного веса грунта
Находим активное давление грунта, полагая что грунт за стенкой приходит в предельное состояние и для точки на глубине z можно написать условие
31
предельного состояния через главные
напряжения, показанные на рис.14. При s1 = gz и s1 > s2 следует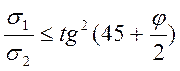 
, но s2 – это давление, которое передается на
грань стенки, тогда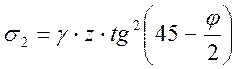 
.
Эпюра s2 имеет вид треугольника, равнодействующая эпюры Еа равна
.
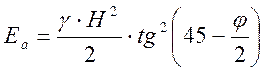Сила Е приложена на высоте H/3 от основания стенки.
Задача 2. Учет нагрузки интенсивностью р на призме обрушения интенсивностью р (рис.14б).
Находим толщину фиктивного слоя грунта по формуле
.
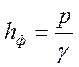В этом случае задача 2 подобна задаче 1, и можно сразу написать величину активного давления - ра = s2 :
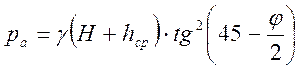, а равнодействующую, равную площади
трапеции, находим по формуле
.
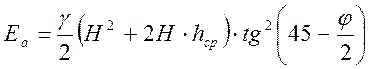Пассивное давление находят, меняя знак в формуле для tg (минус на плюс), тогда
.
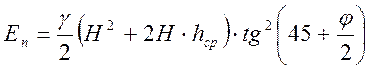Задача 3. Грунт за стенкой глинистый.
В этом случае полагаем, что песчаный грунт работает аналогично глинистому, если
приложить к граням стенки давление связности, равное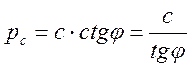 
. Как это делается – показано на
рис.15.
32
Рис.15. Схема определения давления связных грунтов на вертикальную гладкую стенку
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.