График критических напряжений для сжатого стержня. Формула Ясинского для стержней средней гибкости. Условие устойчивости. Коэффициент уменьшения допускаемого напряжения

10. График критических напряжений для сжатого стержня. Формула Ясинского для стержней средней гибкости. Условие устойчивости. Коэффициент уменьшения допускаемого напряжения.

Представим полный график критических напряжений.

 

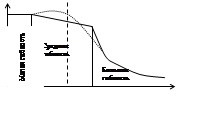
Для стержней очень малой гибкости можно считать, что гибкость равна пределу текучести l=s_Т. Энгессер – предложил простой вариант, провел касательный угол a’ между касательной и e (на диаграмме растяжения). tga’=e - касательный модуль упругости, подставим в формулу для s_КР.

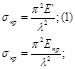Но при начале потери устойчивости – стержень начинает изгибаться. Волокна сжимаются, другие волокна снимают сжатие – уменьшают величину сжатия. Они работают по модулю Е, те что еще больше сжимаются работают по модулю Е’. Значит следует изменить формулу. Где Е_ПР – приведенный модуль упругости, комбинация Е и Е’. Карман (америк. ученый) также предложил этот вариант. Е_ПР – иначе модуль Кармана – Энгессера.

Шенли доказал, что наименьшее значение силы напряжения будет соответственно при использовании касательного модуля напряжения. Формула такая же как и (1). В практических расчетах используют формулу Ясинского. Ее используют для стержней средней гибкости. (l<l_ПР - предельная гибкость).

 Она была получена в результате обработки многочисленных экспериментальных измерений. a и b – приводятся в справочниках для различных материалов, разность напряжения.

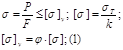Чтобы стержень был устойчивым необходимо, чтобы действующая устойчивость не превышало допускаемое напряжение. К – коэф. запаса прочности. Решили записывать следующим образом (1). j - коэф. снижения основного допускаемого напряжения, тождественен коэф. продольного изгиба. Является функцией от гибкости и материала. Его можно определить по справочнику. Диапазон изменения j от 1 до 0 для стержней бесконечно большой гибкости.

Условие устойчивости формула (2). Проверка устойчивости заданного стержня; Определение наибольшего значения Р, при котором стержень не потеряет устойчивость; Подбор площади поперечного сечения, при котором стержень не потеряет устойчивость; Для сжатых стержней наиболее рационально использовать: круглую или квадратную трубку. Материал: все зависит от Е (у сталей он один). Для стержней большой гибкости материал не важен, можно использовать низкокачественную сталь. Для стержней средней гибкости - смотреть.

11. Проверочный и конструктивный расчет стержня по условию устойчивости.

Расчет производится по формуле:

где F_БР – площадь поперечного сечения стержня без учета ее ослабления.

j - коэф. уменьшения допускаемого напряжения на простое сжатие.

Коэф. j зависит от гибкости l и материала стержня и может быть взят из таблиц.

Условно задачи на устойчивость можно разделить на два типа. К первому относятся задачи, в которых все размеры сечения известны (проверочный). Ко второму относятся такие задачи, в которых необходимо определить размеры сечения.

Первый тип задач. Дано: схема закрепления стержня; l – длина стержня; F – размеры поперечного сечения стержня; [s] – допускаемое напряжение на сжатие для данного материала стержня. Требуется определить допустимую сжимающую нагрузку Р;

Схема решения: По размерам заданного сечения находим Y_MIN и F (минимальный момент инерции и площадь поперечного сечения); потом определяется радиус инерции и вычисляется гибкость:

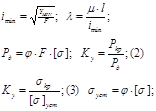Для данного материала находится по таблице коэф. уменьшения допускаемого напряжения j, соответствующий вычисленному значению l. Из формулы (1) определяется допускаемая сила Р; В том случае если требуется одновременно определить коэф. устойчивости К_У, пользуются соотношением (2), в котором Р_Д – допускаемая нагрузка; Р_КР – критическая (Эйлерова) сила. Если Р_КР считать по формуле Эйлера нельзя, то пользуются другим соотношением (3). При этом s_КР для заданного материала находится по формуле Ясинского.