График критических напряжений для сжатого стержня. Формула Ясинского для стержней средней гибкости. Условие устойчивости. Коэффициент уменьшения допускаемого напряжения, страница 3

Теорема о взаимности работ (теорема Бетти).

Работа силы/сил первого состояния на соответствующих обобщенных перемещениях, вызванных силой/силами второго состояния равна работе силы/сил второго состояния на соответствующих обобщенных перемещениях, вызванных силой/силами первого состояния.

1-ое состояние.                                                2-ое состояние.

 

D2,1/(D1,2) – соответствующее перемещение (данное перемещение соответствует силе 2/(1)), вызванное силой 1/(2).

Работа силы Р₁ равна перемещению D1,2 и наоборот    >>>    Р₁*D1,2= Р₂*D2,1;

Чтобы доказать это, вспомним о начале возможных перемещений.

 

Слева – начала возможных перемещений.

V₁/(V₂) – любая из внутренних сил первого состояния/(второго состояния).

Начало возможных перемещений применительно к первому/(второму) состоянию, если считать силы второго/(первого) состояния возможными.

>>>    Р₁*D1,2= Р₂*D2,1 – теорема о взаимности работ доказана.

Впервые была предложена Бетти.

14. Выражение потенциальной энергии деформаций через внутренние силовые факторы. Общая формула для потенциальной энергии деформаций, записанная через обобщенные внутренние силы.

Работа внешних сил в случае упругих деформаций переходит в потенциальную энергию, накопленную в деформированном теле.

Потенциальная энергия накапливается в упругих телах за счет совершением над ними некой работы. Пот. энергия – всегда положительна.

Работа внешних сил – положительна, внутренних – отрицательна.

Пот. энергия – работа внутренних сил взятая с обратным знаком, причем эта работа на действительном перемещении.

 

где Т – обобщенная внешняя сила

U – пот. энергия

Это теорема Клапейрона и одновременно потенциальная энергия для внешних сил.

Для внутренних сил:

где V – обобщенная внутренняя сила

U – пот. энергия

Правая часть интеграла Мора – работа внутренних сил, записанная на возможном перемещении.

Если у нас работа на действительном перемещении, то интеграл Мора записывается следующим образом: (общая формула для определения пот. энергии через внутренние силовые факторы)

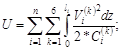
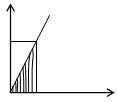
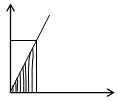
-обобщенный внутренний силовой фактор в произвольном сечении i–го участка сис-мы, имеющего длину l_i и жесткость

 - т.к. грузовое состояние, то появление второго   вызвано перемещением самого ;

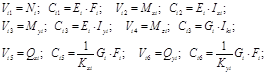
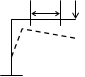15. Метод Максвелла – Мора для определения перемещений. Вывод интеграла Мора.

Общий случай действия сил (6 силовых факторов). Для определения работы внутренних сил будем пользоваться принципом независимости действия сил. Рассмотрим  вначале произвольную плоскую стержневую систему, нагруженную заданными силами.

Осевое растяжение.

Грузовое.                                                           Единичное         

Кручение.         Грузовое                                       Единичное

Изгиб.            Грузовое                                          Единичное

Дифференциальное уравнение изогнутой оси балки.

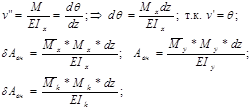
М_у – изгибающий момент в плоскости XoZ.

М_x – изгибающий момент в плоскости YoZ.

М_k – крутящий момент в плоскости XoY.

Грузовое                                          Единичное

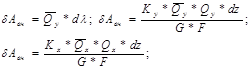
Вместо Е пишем G т.к. речь идет о касательных напряжениях. К_У – коэф. Учитывающий нелинейность распределения касательных напряжений в соответствии с формулой Журавского.

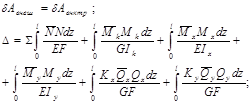
D - обобщенное перемещение. Суммирование идет по всем участкам.

k – номер внутреннего силового фактора, меняется от 1 до 6, т.к. больше 6 внутренних силовых факторов быть не может. I – номер грузового участка, всего n. -обобщенный внутренний силовой фактор в произвольном сечении i–го участка системы, имеющего длину l_i и жесткость ;- тоже, только в единичном состоянии.

Осевое растяжение сжатие. Формула Максвела: