
Лабораторная работа 3.
Часть 1.
Интерполяция.
Выполнил: студент 328гр.
Постановка задачи интерполяции
На интервале [a,b]
задана система точек (узлы интерполяции) Xi, ![]() ;
; ![]() и
значения неизвестной функции в этих узлах
и
значения неизвестной функции в этих узлах ![]()
![]() .
Могут быть поставлены следующие задачи:
.
Могут быть поставлены следующие задачи:
1) Построить функцию F(x),
принимающую в узлах интерполяциизаданные значения ![]() :
: ![]() (условия
интерполяции)
(условия
интерполяции)
2) Для заданного значения ![]() найти
F(z).
найти
F(z).
Решение задачи интерполяции
Задача имеет много решений:
через заданные точки ![]() можно
провести бесконечно много кривых, каждая из которых будет графиком функции, для
которой выполнены все условия интерполяции. Локальная интерполяция: на каждом
интервале
можно
провести бесконечно много кривых, каждая из которых будет графиком функции, для
которой выполнены все условия интерполяции. Локальная интерполяция: на каждом
интервале ![]() строится
своя функция. Глобальная интерполяция: одна функция для всего интервала [a,b]. Пример
локальной интерполяции: Кусочно-линейная. На каждом интервале
функция является линейной
строится
своя функция. Глобальная интерполяция: одна функция для всего интервала [a,b]. Пример
локальной интерполяции: Кусочно-линейная. На каждом интервале
функция является линейной ![]() ; значения
коэффициентов находятся из выполнения условий интерполяции в концах отрезка:
; значения
коэффициентов находятся из выполнения условий интерполяции в концах отрезка: ![]() Итоговая
функция будет непрерывной, но производная будет разрывной в каждом узле интерполяции.
Откуда следует, что
Итоговая
функция будет непрерывной, но производная будет разрывной в каждом узле интерполяции.
Откуда следует, что ![]() если
если
![]() Итоговая
функция будет непрерывной, но производная будет разрывной в каждом узле
интерполяции.
Итоговая
функция будет непрерывной, но производная будет разрывной в каждом узле
интерполяции.
Пример глобальной интерполяции:
полином Лагранжа 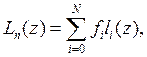 где
где
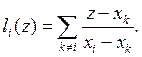
Формулировка задания
1. Задана исходная функция g(x) и
интервал [a,b]. Построить узлы интерполяции ![]() и
вычислить в этих узлах значения
и
вычислить в этих узлах значения ![]() Таким
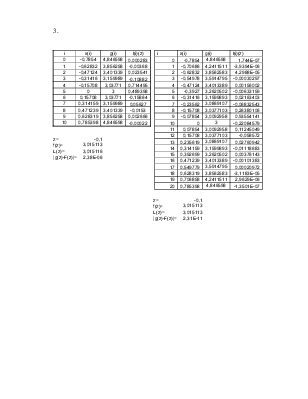
образом, получены исходные данные для задачи интерполяции. Построить график
функции на заданном отрезке.
Таким
образом, получены исходные данные для задачи интерполяции. Построить график
функции на заданном отрезке.
2.Вычислить значение F(z) в
некоторой произвольной точке ![]() не
совпадающей ни с одним из узлов с помощью кусочно-линейной интерполяции. Найти
погрешность метода при N=10 и N=20.
не
совпадающей ни с одним из узлов с помощью кусочно-линейной интерполяции. Найти
погрешность метода при N=10 и N=20.
3. Вычислить значение F(z) с
помощью полинома Лагранжа ![]() где z-произвольная
точка из отрезка
где z-произвольная
точка из отрезка ![]() не
совпадающей ни с одним из узлов. Найти погрешность метода при N=10 и N=20.
не
совпадающей ни с одним из узлов. Найти погрешность метода при N=10 и N=20.
Результаты расчетов.
1.
|
g(x)=3/КОРЕНЬ(1-x^2) |
||
|
i |
x(i) |
g(i) |
|
0 |
-0,785 |
4,846598 |
|
1 |
-0,628 |
3,856258 |
|
2 |
-0,471 |
3,401339 |
|
3 |
-0,314 |
3,159989 |
|
4 |
-0,157 |
3,03771 |
|
5 |
0,000 |
3 |
|
6 |
0,157 |
3,03771 |
|
7 |
0,314 |
3,159989 |
|
8 |
0,471 |
3,401339 |
|
9 |
0,628 |
3,856258 |
|
10 |
0,785 |
4,846598 |
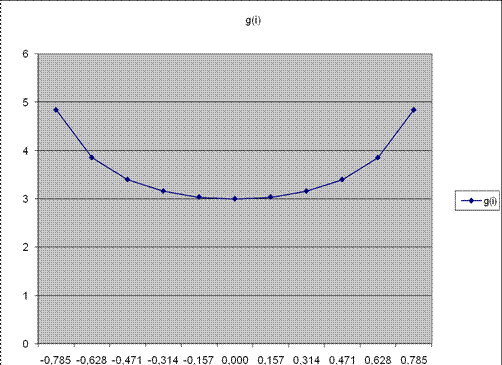
2.
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.