наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию. Чтобы этот тип дифракции осуществить, достаточно точечный источник света поместить в фокусе собирающей линзы, а дифракционную картину исследовать в фокальной плоскости другой собирающей линзы, установленной за препятствием.
Рассмотрим дифракцию Фраунгофера от бесконечно длинной щели (для этого практически достаточно, чтобы длина щели была значительно больше ее ширины). Пусть плоская монохроматическая волна падает нормально плоскости узкой щели шириной d (рисунок 6.1, а).
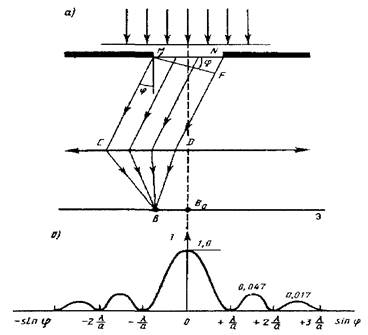
Рис.6.1. К теории дифракции Фраунгофера на одной щели а - падение и ход монохроматической волны на щель, б - дифракционная картина, полученная на экране
Оптическая разность хода между крайними лучами МС и ND, идущими от щели в произвольном направлении j:
(6.1)
где F— основание перпендикуляра, опущенного из точки М на луч ND.
Разобьем открытую
часть волновой поверхности в плоскости
щели MNна зоны
Френеля, имеющие вид полос, параллельных
ребру М щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна ![]() , т.е.
всего на щели уместиться
, т.е.
всего на щели уместиться
![]() зон.
зон.
Так как свет на щель падает нормально, то плоскость щели совпадает с волновым фронтом, следовательно, все точки волнового фронта в плоскости щели будут колебаться в одинаковой фазе. Амплитуды вторичных волн в плоскости щели будут равны, так как выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения. Из выражения (6.1) вытекает, что число зон Френеля, укладывающихся на ширине щели, зависит от угла j. От числа зон Френеля, в свою очередь, зависит результат наложения всех вторичных волн. Из приведенного построения следует, что при интерференции света от каждой пары соседних зон Френеля амплитуда результирующих колебаний равна нулю, так как колебания от каждой пары соседних зон взаимно гасят друг друга. Следовательно, если число зон Френеля четное, то
![]() (6.2)
(6.2)
и в точке В наблюдается дифракционный минимум (полная темнота), если же число зон Френеля нечетное, то
(6.3)
и наблюдается дифракционный максимум, соответствующий действию одной некомпенсированной зоны Френеля. Отметим, что в направлении j = 0 щель действует как одна зона Френеля, и в этом направлении свет распространяется с наибольшей интенсивностью, т.е. в точке В0 наблюдается центральный дифракционный максимум. Из условий (6.2) и (6.3) можно найти направления на точки экрана, в которых амплитуда (а, следовательно, и интенсивность) равна нулю или максимальна. Распределение интенсивности на экране, полученное вследствие дифракции (дифракционный спектр), приведено на рисунке 6.1, б.
Из опыта и соответствующих расчетов следует, что сужение щели приводит к тому, что центральный максимум расплывается, а интенсивность уменьшается (это, естественно, относится и к другим максимумам). Наоборот, чем щель шире (d > λ), тем картина ярче, но дифракционные полосы уже, а число самих полос больше.
Для прямого наблюдения дифракции Фраунгофера предлагается схема рисунка 6.2.
Положение нулей интенсивности Хт в дифракционной картинке, наблюдаемой на экране Э, согласно (6.2) определяется равенством:
![]()
(6.4)
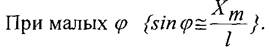
Из (6.4) видно, что расстояние между нулями интенсивности обратно пропорционально ширине d щели, но прямо пропорционально порядку дифракции m и расстоянию l.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
В работе экспериментально определяются размеры щелей по результатам дифракционной картины на них и сравниваются с прямыми измерениями.
Описание установки
В работе для проведения опытов используется полупроводниковый лазер с длиной волны 670 нм (излучение красного цвета). В корпус лазера вмонтирована специальная оптика, коллимирующая параллельный пучок. Лазер имеет отдельный блок питания, который подключается к напряжению 220В, 50 Гц и имеет небольшие размеры. Хорошее качество излучения и малые габариты делают использование полупроводникового лазера более предпочтительным, чем использование других исторически традиционных способов получения монохроматического излучения.
Лабораторная работа выполняется на установке, оптическая схема которой приведена на рисунке 6.2. Она включает в себя источник света 1 (лазер), объект исследования (щель) 2, экран 5. Кассета с объектом крепится на рейтере 4 и устанавливается в паз 3 на оптической скамье. На экране, который жестко закреплен на противоположном от источника света конце оптической скамьи, магнитами закрепляется чистый лист бумаги для зарисовки дифракционной картины.
Порядок выполнения работы
1. Включить лазер и его луч направить в центр экрана.
2. Поставить на пути луча одну из двух предлагаемых щелей и добиться, чтобы светлое пятно размещалось в центре щели
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.