Формирование рациональной структуры операции

11 Научно-исследовательская часть

   Тема данной работы: «Формирование рациональной структуры операции».

   Выбор рациональной последовательности установов и переходов операции является многовариантной задачей, решение которой проводится последовательно на всех этапах проектирования технологических процессов.

   Полученные наборы переходов для элементарных поверхностей, а так же заданные техническими условиями точностные параметры их формы, размеров и положение, которые необходимо обеспечить в процессе обработки, является совместно с данными о размерно-точностных характеристиках заготовки исходными условиями для формирования структуры операции.

   Критериями оценки вариантов проектируемой операции является штучное время обработки Т_шт или себестоимость ее выполнения С, величины которых уменьшаются при сокращении числа переходов, при одновременном их выполнении или совмещении элементов основного и вспомогательного времени.

   Число переходов прежде всего зависит от числа ступеней обработки каждой элементарной поверхности детали, необходимого для перевода ее из состояния заготовки в конечное – заданное чертежом. Чем меньше ступеней обработки требуется для каждой поверхности, тем больше возможностей сокращения времени выполнения операции.

11.1 Выбор оптимального маршрута обработки поверхностей детали    

   Практическое решение данной задачи показывает, что она довольно сложна даже при незначительном числе рабочих ходов инструмента. При обработке наружных и внутренних поверхностей в зависимости от квалитетов точности и шероховатости может возникать большое количество вариантов.

   Использование математического аппарата теории графов позволяет избежать полного перебора вариантов маршрута и в тоже время получить оптимальный по некоторому критерию маршрут. Для этой цели наиболее подходящим критерием является  себестоимость обработки отдельной поверхности.

   В качестве исходных данных принимается ТТ, предъявляемые к поверхностям детали во всех ее состояниях обработки, включая заготовку; оборудование, необходимое для обработки поверхностей; оперативное время каждого рабочего хода инструмента.

   При решении рассматриваемой задачи принимаются следующие ограничения:

-  поверхности, обрабатываемые одним инструментом, за один прием, заменяются одной комплексной;

-  себестоимость обработки каждой поверхности на конкретном технологическом переходе не зависит от ее места в общей последовательности обработки;

-  принятое из множества возможных последовательность обработки по технологическим переходам должна обеспечивать экономическую точность и шероховатость поверхности.

Для решения задачи разрабатывается математическая модель технологического маршрута. Все варианты последовательностей объединяются в графы возможного маршрута W (см. рисунок 11.1).

Рисунок 11.1 – Исходный граф возможного маршрута W

   Вершины Р­i графа W – технологические переходы по обработке поверхности на каждом этапе, которые называются элементами маршрута обработки. Дугами w_ij графа W являются характеристики последовательности обработки. В качестве последних принимается функция w_ij , которая равна единице, если элемент j может обрабатываться после элемента i, и равна 0 в противном случае. Граф W представляется в  виде матрицы смежности W^s.

   Каждая поверхность может проходить несколько этапов обработки от Э₀ до Э_к . Тогда число вершин графа равно сумме всех элементов обработки и определяется как сумма этапов по всем обрабатываемым поверхностям:

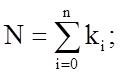                                                                                                 (11.1)

где k_i – число этапов обработки i-ой поверхности.

   На следующем этапе решения поставленной задачи необходимо формализовать ограничения, накладываемые технологическим процессом. На пример, при механической обработке резанием нельзя снять нижний слой припуска, если еще не снят верхний. Это значит, что дуга w_il,jr , соединяющая элементы Р_il, Р_jr (1 – ый индекс – номер поверхности, второй – номер этапа ее обработки), может быть реализована только в случае, если обработаны все элементы Р­_iv­ для v<l и Р_jw для w<r.

   На каждом этапе поверхности отождествляются с элементами графа W по уровню этапа. Предыдущие  элементы поверхности, вошедшие в предлагаемый  маршрут, могут быть исключены из рассмотрения. В графе W обращение к цепочки элементов одной поверхность производится последовательно от верхнего уровня к нижнему. Обращение возможно только к верхнему элементу, после чего он не рассматривается. Такая система доступа соответствует стековой организации хранения и обработки информации.

   Если в математической модели движения поверхности вниз по этапам обработки заменить движением элементов данной поверхности вместе с их связями вверх по уровням графа W таким образом, что верхний элемент стека поверхности всегда находится на уровне Э₀, то когда из графа W (см. рисунок 11.1) выбрать элемент Р₂₀ граф примет вид, показанный на рисунке 11.2.

Рисунок 11.2 – Граф возможного маршрута W после выборки элемента Р₂₀

   Далее необходимо определить анализируемое ограничение в рамках разрабатываемой математической модели. Дуги графа возможного маршрута для построения дерева оптимального маршрута М можно выбирать только на верхнем уровне графа W.

   Для математического выражения данного ограничения вводим матрицу ограничений G с такой же структурой, как у матрицы смежности W^S графа W. Каждый элемент g_ij матрицы G равен 0, если для выборки j-го элемента графа необходимое условие – предварительная выборка i-го элемента. В противном случае g_ij равен единице. Так , для графа на рисунке 11.2 матрица G имеет следующий вид:

                                                       10  1i   20  2i  2k

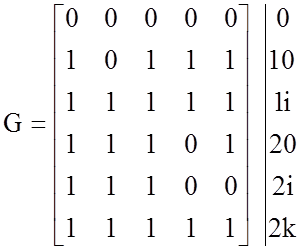
                                                                      (11.2)

   После выборки каждого элемента графа W матрица G модифицируется и строка, соответствующая выбранному элементу, устанавливается на место единицы. Для определения графа R верхнего уровня, который является подграфом графа возможного маршрута, необходимо и достаточно выполнить поэлементное логическое умножение матрицы ограничение G и матицы смежности W^s:

                                                                                            (11.3 )

где R^s – матрица смежности графа R.

   Полученная математическая модель технологического маршрута, состоящая из графа возможного маршрута и матрицы ограничений, отражает структурные связи. Но так как последние обуславливают эффективность технологического маршрута, представленная математическая модель может быть использована для выбора оптимального маршрута.

   Далее производится выбор оптимального с точки зрения себестоимости цикла обработки. При этом затраты на переход от предыдущего элемента к следующему без смены рабочего места можно определить по формуле:

                                                                                  (11.4)

где t_ij – время перехода между i-ым и j-ым переходами;

      С­_мч – стоимость одного машино-часа;

      З_р – почасовые затраты на заработную плату обслуживающего персонала.

  Затраты на переход от предыдущего элемента к следующему при смене оборудования:

                                                                                    (11.5)

где С_i – себестоимость работ, выполняемых после окончания  i-го элемента (до готовности рабочего места начинать подготовку к приему следующего элемента);

      С_j – себестоимость работ от момента начала подготовки рабочего места к приему i-го элемента до начала обработки j-го элемента;

      З_ij – cебестоимость транспортировки детали от рабочего места, на котором осуществляется i-ый элемент, до рабочего места, где реализуется j-ый элемент.

   Значения С_i , С_j устанавливаются аналогично .

    Рассмотренная методика выбора оптимального маршрута обработки поверхностей детали пригодна и при использовании других критериев оптимальности.

11.2 Составление вариантов последовательности установов и переходов операции

   После выбора оптимального маршрута обработки отдельных поверхностей детали можно приступать к оптимизации структуры самой операции.