Параметрические колебания нелинейных систем. Параметрический резонанс и параметрическая неустойчивость в линейной системе

Лекция 16

Параметрические колебания нелинейных систем

Параметрический резонанс и параметрическая неустойчивость в линейной системе

Специфическим видом внешнего воздействия на колебательную систему является периодическое изменение параметров системы во времени. Такое воздействие называется параметрическим. Начнем с краткого напоминания об основных особенностях параметрических колебаний в линейных системах^[1].

Рассмотрим простую модельную систему: колебательный контур с переменной емкостью (рис. 16.1). Изменение емкости со временем можно обеспечить, например, механически изменяя расстояние между пластинами конденсатора. В таком случае мгновенные значения заряда q и напряжения u на емкости будут связаны соотношением q t( ) = C t u t( ) ( ) . Это позволяет записать дифференциальное уравнение, описывающее колебания в контуре

                                                               q ^{+    1}     q = 0.                                           (16.1)

LC(t)

Уравнение (16.1) имеет вид уравнения гармонического осциллятора, собственная частота которого зависит от времени.

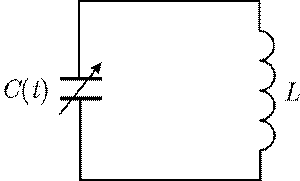
Рис. 16.1. Колебательный контур с переменной емкостью

Пусть емкость конденсатора изменяется следующим образом. В моменты времени, когда заряд на конденсаторе максимален, пластины резко раздвигаются. При этом емкость уменьшается от некоторого значения C₂ до значения C₁ < C₂. Поскольку заряд на конденсаторе при этом не изменяется, напряжение скачком возрастет от значения V₂ до значения V₁ = C_{2 2}V C₁ . В моменты времени, когда заряд равен нулю, пластины так же резко сдвигаются; емкость при этом увеличивается, а напряжение остается равным нулю (рис. 16.2). В таком процессе постоянно совершается работа, которая идет на увеличение энергии колебаний. За один период приращение энергии составит (необходимо учесть, что в течение периода пластины раздвигаются дважды)

                             ∆W = 2(W₁ −W₂) = CV_{1 1}² −C V_{2 2}² = C V_{2 2}² ^{ C2} −1^.         (16.2)

                                                                                                                              C₁        

Если ввести обозначения ∆C = C₂ −C₁, C = (C₁ +C₂)2 и считать, что ∆C C , соотношение (16.2) можно переписать в виде

                                                                 .                                            (16.3)

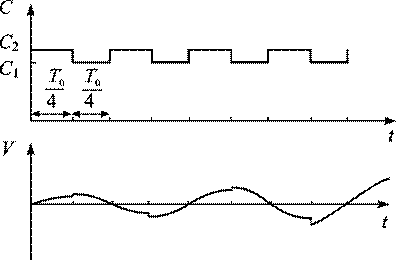
Рис. 16.2. Зависимость от времени емкости и напряжения в колебательном контуре с механически перестраиваемым конденсатором

Из приведенных выше рассуждений следует, что для эффективного поступления энергии в систему период колебаний T₀ и период изменения параметра T должны быть связаны соотношением

                                                                      T ,                                                   (16.4)

которое представляет собой условие параметрического резонанса. Отметим отличие от резонансного условия при вынужденных колебаниях линейного осциллятора, T ≈T₀.

Можно, однако, раздвигать пластины не каждый раз, когда заряд на конденсаторе максимален, а через раз; энергия все равно будет поступать в систему, хотя и в меньшем количестве. Более того, очевидно, что это можно делать в общем случае только в каждый n-ный благоприятный момент. Таким образом, имеется, вообще говоря, бесконечное число параметрических резонансов, условия которых имеют вид

                                                                    T  ,.                                                (16.4)

Число n =1,2,… будем называть порядком резонанса, а резонанс при n =1 — основным.

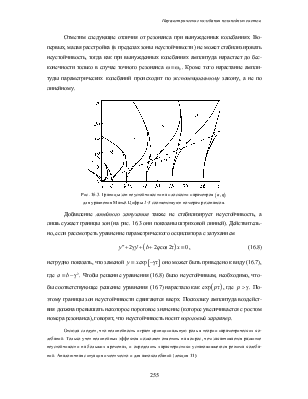
При выполнении условий резонанса колебания в линейной системе, как можно видеть на рис. 16.2, неограниченно нарастают. Это явление называется параметрической неустойчивостью.

Основной моделью в теории параметрических колебаний в линейных системах служит уравнение Матьё 

                                                       x + ω₀²(1+ f cosωt)x = 0 ,                                   (16.5)

которое представляет собой уравнение линейного осциллятора с гармоническим параметрическим возбуждением. Это уравнение детально исследовано математиками; более того, его решения составляют особый класс специальных функций — функции Матьё. Для наших дальнейших целей важно отметить следующие его свойства. На плоскости параметров амплитуда — частота воздействия существуют зоны неустойчивости, которые имеют вид характерных клювов, расположенных в окрестности резонансных частот

                                                                     .                                                 (16.6)

Перейдем к новой независимой переменной τ = ωt2 . Тогда уравнение (16.5) можно переписать в виде

                                                        x′′+(a + 2qcos2τ) x = 0,                                   (16.7) где a = ω4 ₀²ω² , q = ω2 ₀² f ω² , штрихи обозначают дифференцирование по τ. Зоны неустойчивости на плоскости параметров (a q, ) изображены