Исследование характеристик систем, образованных последовательным и параллельным соединениями звеньев в корневой, временной и частотной областях

Лабораторная работа №2

Содержание

Цель: Исследование характеристик систем, образованных последовательным и параллельным соединениями звеньев в корневой, временной и частотной областях.

Задача 2.1. Определить характеристики в корневой, временной и частотной областях последовательного соединения двух устойчивых апериодических звеньев первого порядка  и  с параметрами , , ,  соответственно (см. варианты заданий).

Рассчитать параметры  ПФ эквивалентного звена второго порядка, записанной в виде:

.

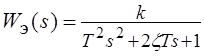Решение: Учитывая значения ,  и  , , покажем вид передаточных функций двух устойчивых апериодических звеньев первого порядка: 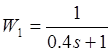; ;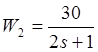тогда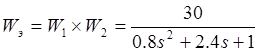

Тогда  (сек), , .

На рисунке 1 показаны нули и полюсы двух апериодических звеньев первого порядка

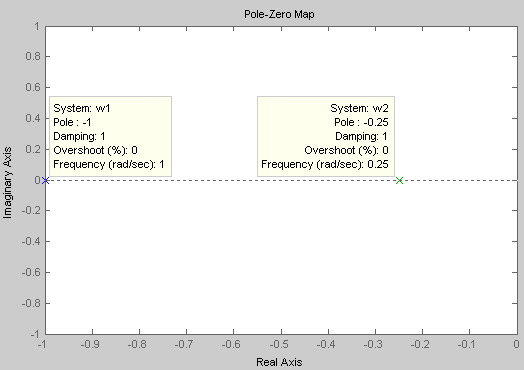
Рис.1 Нули и полюсы двух апериодических звеньев первого порядка

На рисунке 2 показаны ЛАЧХ и ЛФЧХ двух апериодических звеньев первого порядка

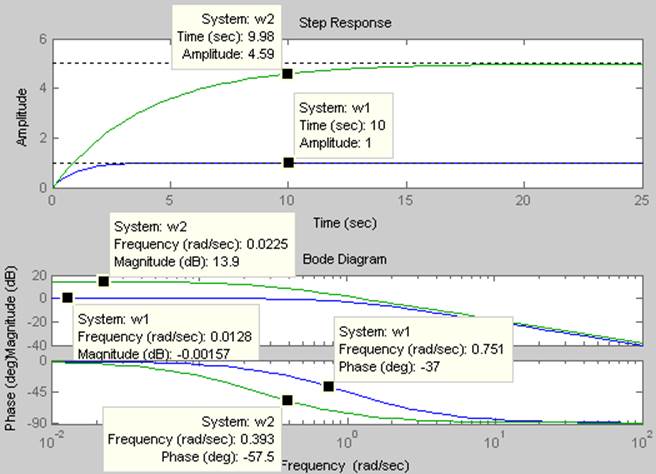
Рис.2 ЛАЧХ и ЛФЧХ двух апериодических звеньев первого порядка

На рисунке 3 показаны характеристики в частотной области двух апериодических звеньев первого порядка

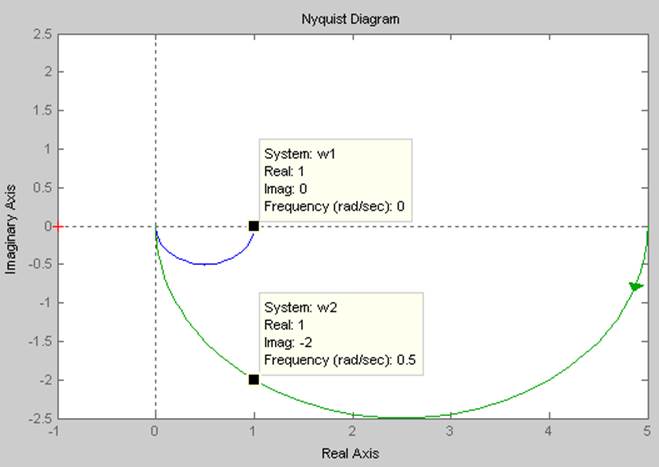
Рис. 3 Частотные области двух апериодических звеньев первого порядка

Ответить на следующие вопросы:

Какой вид имеет асимптотическая логарифмическая амплитудно-частотная характеристика (ЛАЧХ) соединения (привести график)?

Ответ: На рисунке 4 показана асимптотическая логарифмическая амплитудно-частотная характеристика (ЛАЧХ) соединения

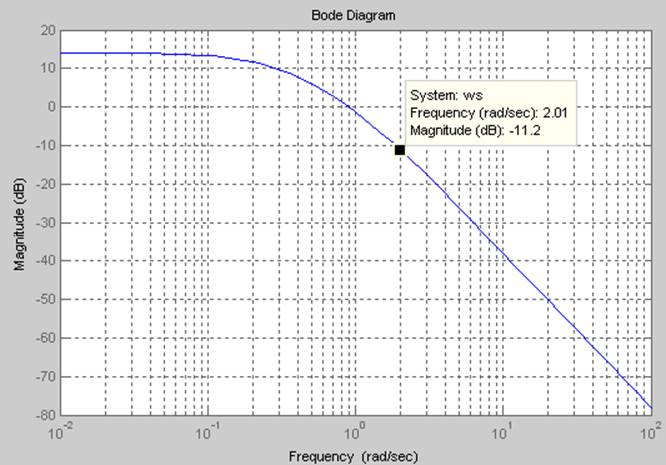
Рис. 4 Асимптотическая логарифмическая амплитудно-частотная характеристика (ЛАЧХ) соединения

В чём состоят различия переходных и частотных (амплитудно-фазовых характеристик (АФХ), логарифмических частотных характеристик (ЛЧХ)) характеристик апериодического звена  и соединения звеньев ? Привести графики и дать подробный анализ. При анализе обратить внимание: на производные переходных характеристик в нуле, на их установившиеся значения; на длительность переходных процессов; на то, в каких квадрантах комплексной плоскости располагаются АФХ; чем отличаются ЛЧХ на низких и высоких частотах; по ЛАЧХ сравнить фильтрующие свойства  и .

Ответ: Нужные графики апериодического звена приведены на рисунках 2 и 3, график ЛАЧХ приведён на рисунке 4, а графики переходной характеристики, ЛФЧХ и АФХ приведены ниже.

На рисунке 5 изображён график переходной характеристики соединения звеньев

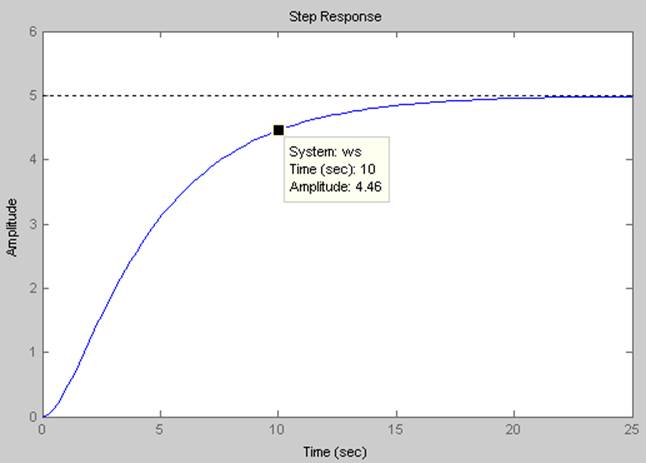
Рис. 5 Переходная характеристика соединения звеньев

На рисунке 6 изображён график ЛФЧХ соединения звеньев

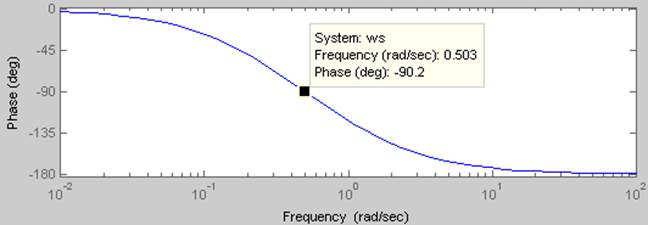
Рис. 6 ЛФЧХ соединения звеньев

На рисунке 7 изображён график АФХ соединения звеньев

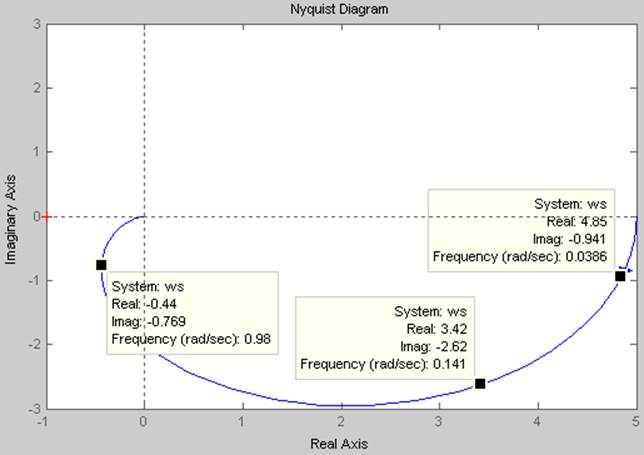
Рис. 7 АФХ соединения звеньев

Как показано на рисунках, на частотах больше k/T ЛАЧХ звена  убывает в два раза быстрее, чем ЛАЧХ звена W1, значит полоса пропускания фильтра  меньше, чем у фильтра .

На низких частотах (при частоте  < 0,1/T) ЛАЧХ звеньев отличаются на постоянную величину (20дБ). На графиков ЛАЧХ на рисунке 1.2 видно, что звено  проявляет усилительные свойства на малых частотах, а звено  ведет себя как неискажающее.

АФХ лежит в IV квадрате комплексной плоскости, а АФХ лежит в III и в IV квадратах комплексной плоскости.

Какое из двух звеньев  и  оказывает большее влияние на длительность затухания переходного процесса и почему?

Ответ: Чем больше значение постоянной времени T, тем дольше устанавливается процесс. Следовательно,  оказывает большее влияние на длительность затухания переходного процесса.

Задача 2.2. Определить характеристики в корневой, временной и частотной областях последовательного соединения двух звеньев с ПФ

,           .

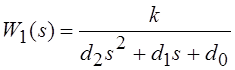Значения параметров ПФ звеньев: , , , ,  

Решение: Приведём и .

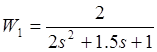
Тогда будет выглядеть:  ;

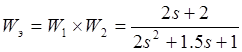На рисунке 8 показаны нули и полюсы звена с ПФ

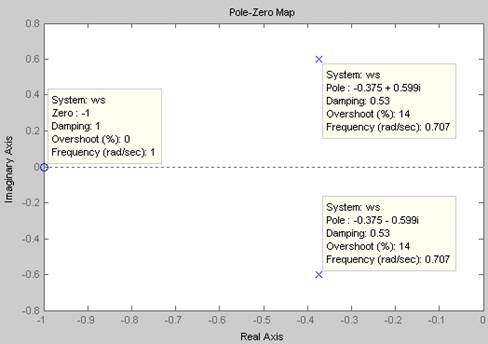
Рис. 8 Нули и полюсы звена с ПФ

На рисунке 9 показаны временные характеристики звена с ПФ

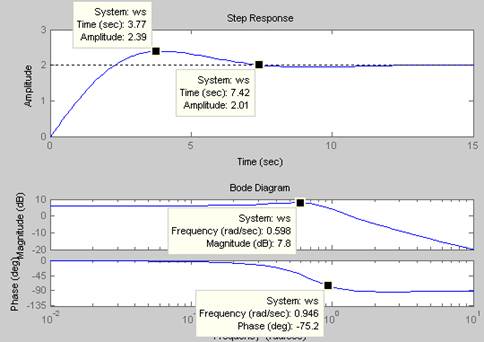
Рис. 9 Временные характеристики звена с ПФ

На рисунке 10 показано АФХ звена с ПФ

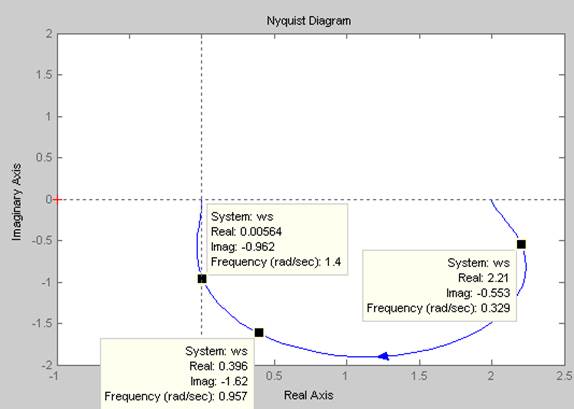
Рис. 10 АФХ звена с ПФ

Ответить на следующие вопросы:

Какому типовому звену соответствуют переходная и частотные характеристики соединения?

Ответ: Переходная и частотные характеристики соединения соответствуют звену второго порядка, описываемое дифференциальным уравнением 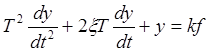, с параметрами

Является ли система второго порядка с ПФ  полностью управляемой и наблюдаемой? Объяснить почему.

Решение:  ПФ эквивалентного звена:

ПФ эквивалентного звена:

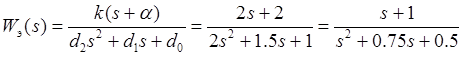
Представим систему в форме пространства состояний (ФПС).

А – матрица состояний (в форме Фробениуса);