Рис.
22 Переходные характеристики звена с ПФ 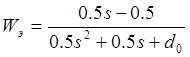 при изменении
при изменении ![]()
w:
![]() =-1 , w1:
=-1 , w1:
![]() =-1.5 , w2:
=-1.5 , w2:
![]() =-0.5.
=-0.5.
Выводы:
1) При ненулевых начальных условиях система становится неустойчивой, переходная характеристика меняется (увеличение).
2) При малых возмущениях система остаётся устойчивой, но значительно падает амплитуда сигнала.
3) При изменении ![]() система
становится неустойчивой, при d2 < 0.5 стремление
переходной характеристики к +
система
становится неустойчивой, при d2 < 0.5 стремление
переходной характеристики к +![]() происходит
быстрее, чем при d2 > 0.5.
происходит
быстрее, чем при d2 > 0.5.
При d1
< 0.5 переходная характеристика стремится к +![]() быстрее, чем при d1
> 0.5. Аналогично при изменении коэффициента d2.
быстрее, чем при d1
> 0.5. Аналогично при изменении коэффициента d2.
При d0
< -1 переходная характеристика стремится к +![]() быстрее, чем при d0
> -1. Аналогично при изменении коэффициента d2
и d1.
быстрее, чем при d0
> -1. Аналогично при изменении коэффициента d2
и d1.
Как отражается на характеристиках соединения с ПФ ![]() в корневой, временной и
частотной областях неполная компенсация неустойчивого полюса ПФ
в корневой, временной и
частотной областях неполная компенсация неустойчивого полюса ПФ ![]() (неполная компенсация
происходит в том случае, когда соответствующие нуль и полюс не совпадают, хотя
могут быть близкими, т. е. располагаться на плоскости корней друг относительно
друга на сколь угодно малом расстоянии)?
(неполная компенсация
происходит в том случае, когда соответствующие нуль и полюс не совпадают, хотя
могут быть близкими, т. е. располагаться на плоскости корней друг относительно
друга на сколь угодно малом расстоянии)?
Ответ: При
![]() ,
тогда
,
тогда 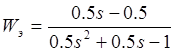 .
.
Возьмём ![]() ,
тогда
,
тогда 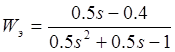 .
.
Возьмём ![]() ,
тогда
,
тогда 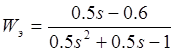 .
.
На рисунке 23 показан график переходной
характеристики ![]() при полной
компенсации неустойчивого полюса
при полной
компенсации неустойчивого полюса ![]() , график
переходной характеристики
, график
переходной характеристики ![]() с неполной
компенсацией неустойчивого полюса
с неполной
компенсацией неустойчивого полюса ![]() ,
, ![]() ,
график переходной характеристики
,
график переходной характеристики ![]() с неполной
компенсацией неустойчивого полюса
с неполной
компенсацией неустойчивого полюса ![]() ,
,![]() .
.
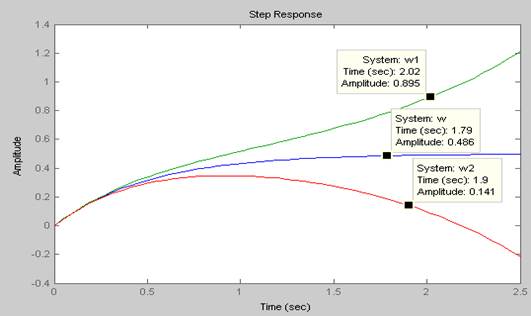
Рис.
23 Переходная характеристика ![]() при полной
(
при полной
(![]() ) и неполной (
) и неполной (![]() и
и ![]() )компенсации
неустойчивого полюса
)компенсации
неустойчивого полюса ![]()
График переходной характеристики
существенно меняется, при ![]() процесс
становится неустойчивым, амплитуда увеличивается, при
процесс
становится неустойчивым, амплитуда увеличивается, при ![]() процесс
остаётся не устойчивым, но амплитуда уменьшается.
процесс
остаётся не устойчивым, но амплитуда уменьшается.
На рисунке 24 показан график ЛАЧХ ![]() при полной компенсации
неустойчивого полюса
при полной компенсации
неустойчивого полюса ![]() , график ЛАЧХ
, график ЛАЧХ ![]() при неполной компенсации
неустойчивого полюса
при неполной компенсации
неустойчивого полюса ![]()
![]() ,
график ЛАЧХ
,
график ЛАЧХ ![]() при неполной компенсации
неустойчивого полюса
при неполной компенсации
неустойчивого полюса ![]()
![]() .
.
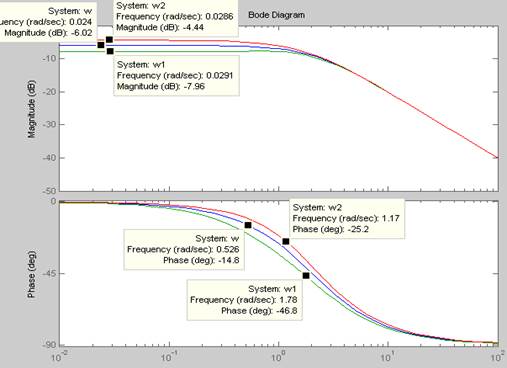
Рис.
24 ЛАЧХ и ЛФЧХ ![]() при полной (
при полной (![]() ) и неполной (
) и неполной (![]() и
и ![]() )компенсации
неустойчивого полюса
)компенсации
неустойчивого полюса ![]()
При ![]() ,
ЛАЧХ уменьшается, ЛФЧХ,
,
ЛАЧХ уменьшается, ЛФЧХ, ![]() .
.
На рисунке 25 показан график АФХ ![]() при полной компенсации
неустойчивого полюса
при полной компенсации
неустойчивого полюса ![]() , график АФХ
, график АФХ ![]() при неполной компенсации
неустойчивого полюса
при неполной компенсации
неустойчивого полюса ![]()
![]() ,
график АФХ
,
график АФХ ![]() при неполной компенсации
неустойчивого полюса
при неполной компенсации
неустойчивого полюса ![]()
![]() .
.
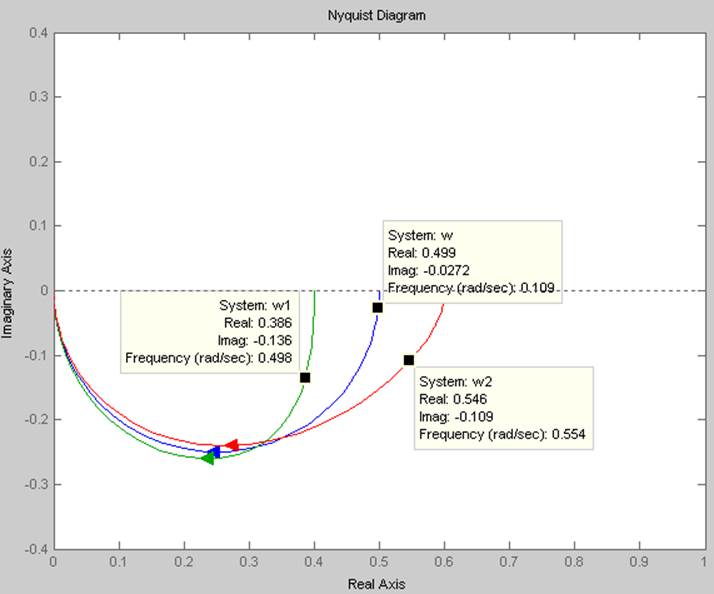
Рис.
25 АФХ ![]() при полной (
при полной (![]() ) и неполной (
) и неполной (![]() и
и ![]() )
компенсации неустойчивого полюса
)
компенсации неустойчивого полюса ![]()
Задача
2.4. Найти ПФ ![]() типовых
звеньев, параллельные соединения которых описываются эквивалентными
дифференциальными уравнениями вида:
типовых
звеньев, параллельные соединения которых описываются эквивалентными
дифференциальными уравнениями вида:
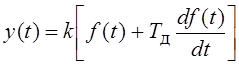 ;
;
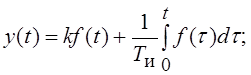
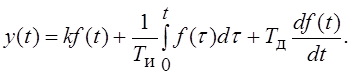
Определить частотные характеристики эквивалентных звеньев. Построить их точные и асимптотические ЛАЧХ, а также логарифмические фазочастотные характеристики (ЛФЧХ). Что можно сказать о фильтрующих свойствах соединений на низких и высоких частотах?
Решение:
Передаточная функция первого звена будет
иметь вид ![]() ,
второго звена
,
второго звена 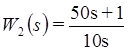 , а третьего
, а третьего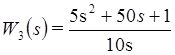 .
.
1)
ЛАЧХ первого эквивалентного звена ![]() .
.
ЛФЧХ будет иметь вид ![]() .
.
Частотные характеристики приведены на рисунках 26 и 27.
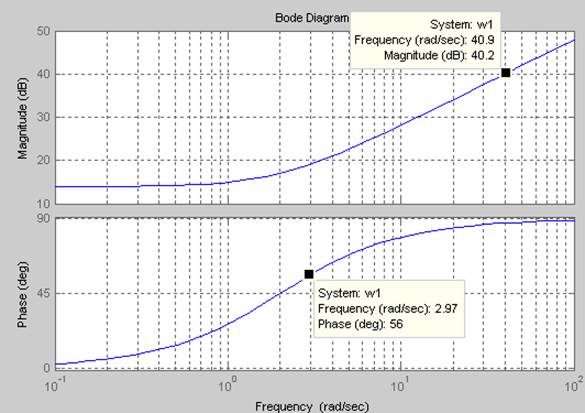
Рис 26 ЛАЧХ И ЛФЧХ первого эквивалентного звена
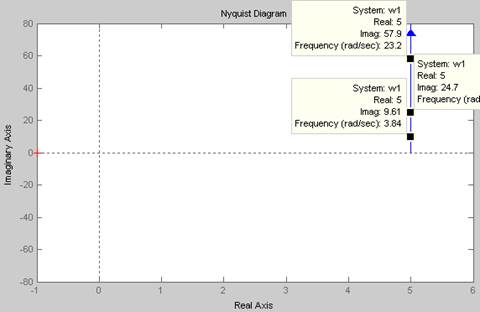
Рис. 27 АФХ первого эквивалентного звена
Из графиков ЛЧХ на рисунке 26 видно, что
рассматриваемое эквивалентное звено пропускает нижние частоты без запаздывания
и без усиления, а входной сигнал высокой частоты на выходе усиливается и
опережает исходный на ![]() . Можно сделать
вывод, что данное звено является фильтром высоких частот.
. Можно сделать
вывод, что данное звено является фильтром высоких частот.
2)ЛАЧХ
второго эквивалентного звена ![]() . ЛФЧХ будет иметь
вид
. ЛФЧХ будет иметь
вид 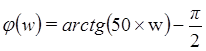 .
Частотные характеристики второго звена изображены на рисунках 28 и 29.
.
Частотные характеристики второго звена изображены на рисунках 28 и 29.
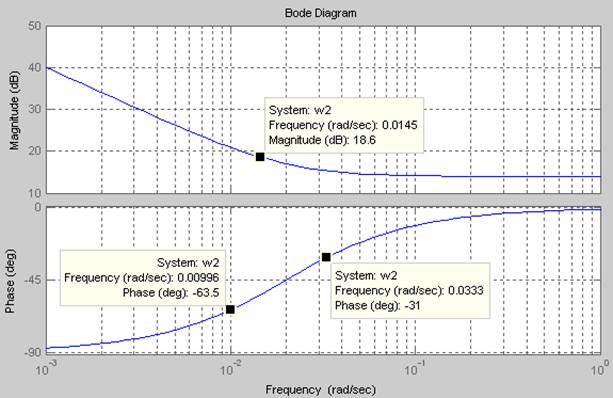
Рис. 28 ЛАЧХ и ЛФЧХ второго эквивалентного звена
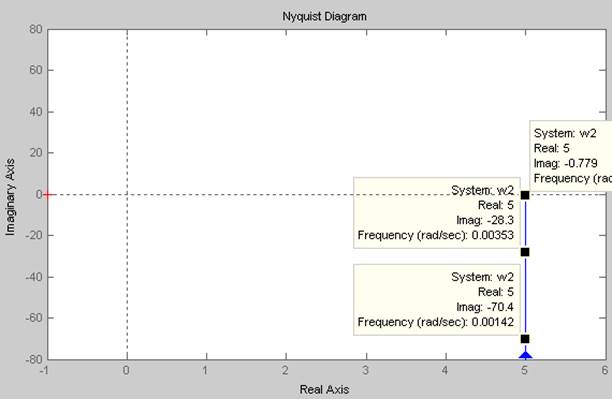
Рис. 29 АФХ второго эквивалентного звена
На рисунке 28 изображены ЛАЧХ второго
эквивалентного звена, который является фильтром низких частот, так как звено
усиливает нижние частоты и без изменения пропускает высокие частоты, причём на
выходе нижние частоты запаздывают на ![]() , а высокие
проходят без сдвига по фазе.
, а высокие
проходят без сдвига по фазе.
ЛФЧХ будет иметь вид 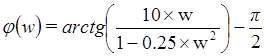 . Частотные характеристики третьего
звена изображены на рисунках 30 и 31.
. Частотные характеристики третьего
звена изображены на рисунках 30 и 31.
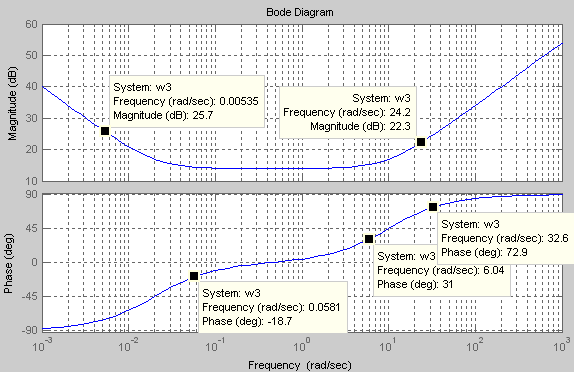
Рис. 30 ЛАЧХ и ЛФЧХ третьего эквивалентного звена
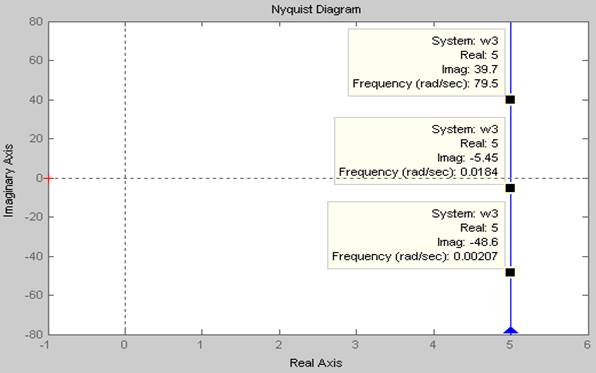
Рис. 31 АФХ третьего эквивалентного звена
Анализируя графики ЛЧХ третьего
эквивалентного звена можно сказать, что звено усиливает низкие и высокие
частоты, при этом пропуская без усиления средние частоты в диапазоне от 0,1 до
10. Низкие частоты запаздывают, а высокие частоты опережают исходный сигнал на ![]() . Таким образом,
третье звено является режекторным фильтром.
. Таким образом,
третье звено является режекторным фильтром.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.