
ПРИМЕР 5
РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА
Постановка задачи
Дано дифференциальное уравнение ![]() . Необходимо найти его решение
методами Эйлера, усовершенствованным Эйлера, модифицированным Эйлера и
Рунге-Кутта четвертого порядка при заданных начальных условиях y(x0)=y0 на заданном промежутке интегрирования [xНАЧ,хКОН] с шагом, вычисленным по формуле: h=(xКОН-хНАЧ)/20.
. Необходимо найти его решение
методами Эйлера, усовершенствованным Эйлера, модифицированным Эйлера и
Рунге-Кутта четвертого порядка при заданных начальных условиях y(x0)=y0 на заданном промежутке интегрирования [xНАЧ,хКОН] с шагом, вычисленным по формуле: h=(xКОН-хНАЧ)/20.
В качестве результата требуется сформировать таблицу, содержащую следующие графы:
1) значения аргумента х;
2) решение, полученное методом Эйлера;
3) решение, полученное усовершенствованным методом Эйлера;
4) решение, полученное модифицированным методом Эйлера;
5) решение, полученное методом Рунге-Кутта 4-го порядка;
6) ошибка метода Эйлера по сравнению с методом Рунге-Кутта.
Пример выполнения работы
Порядок выполнения работы поясним на конкретном
примере. Создадим электронную таблицу для решения дифференциального уравнения ![]() при начальных условиях y(0)=1 на промежутке [0, 0.7].
при начальных условиях y(0)=1 на промежутке [0, 0.7].
Общее решение данного уравнения имеет следующий аналитический вид: y=tg(x+C)-x.
Введем заголовки таблицы и исходные данные:
A1¬’РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
A2¬’Начальные условия: D2¬’Xo= E2¬0 F2¬’Yo= G2¬1
I 2¬’Уравнение: y’=(x+y)^2
A3¬’Промежуток интегрирования: D3¬’Хн= E3¬0 F3¬’Хк= G3¬0,77
A4¬’Шаг интегрирования: D4¬’H= E4¬=(G3-E3)/20
Построим таблицу изменения аргумента Х:
A5¬’Х A6¬=E3 A7¬=A6+$E$4 . Копируем А7 в А8:А26 .
Построим таблицу решения уравнения по методу Эйлера:
B5¬’Эйлер B6¬=G2 B7¬=B6+$E$4*(A6+B6)^2 . Копируем B7 в B8:B26 .
Построим таблицу решения уравнения по усовершенствованному методу Эйлера:
C5¬’Эйл.ус. С6¬=G2 С7¬=C6+0,5*$E$4*((A6+C6)^2+(A7+C6+$E$4*(A6+C6)^2)^2) .
Копируем С7 в С8:С26 .
Построим таблицу решения уравнения по модифицированному методу Эйлера:
D5¬’Эйл.мод. D6¬=G2 D7¬=D6+$E$4*(A6+0,5*$E$4+D6+$E$4/2*(A6+D6)^2)^2 .
Копируем D7 в D8:D26 .
Построим таблицу решения уравнения по методу Рунге-Кутта 4 порядка:
E5¬’K0 F5¬’K1 G5¬’K2 H5¬’K3 I 5¬’РунгеКутт I 6¬=G2
E7¬=$E$4*(A6+I6)^2 F7¬=$E$4*(A6+0,5*$E$4+I6+0,5*E7)^2 G7¬=$E$4*(A6+0,5*$E$4+I6+0,5*F7)^2 H7¬=$E$4*(A6+$E$4+I6+G7)^2
I 7¬=I6+(E7+2*F7+2*G7+H7)/6
Копируем E7: I 7 в E8: I 26 .
Построим таблицу ошибок метода Эйлера по сравнению с методом Рунге-Кутта на каждом шаге интегрирования:
J5¬’Ош.ЭЙЛ J6¬=ABS(J6-I6) . Копируем J6 в J7:J26 .
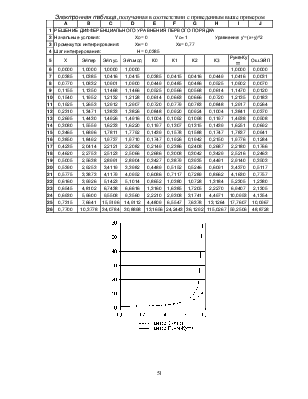
Построим совместные графики «метод Эйлера– метод Рунге-Кутта».
Электронная таблица, полученная в соответствии с приведенным выше примером
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.