Уточненный расчет валов. Силы в зацеплении. Расчетная схема ведущего вала. Суммарные реакции в опорах. Расчетная схема промежуточного вала

Рисунок 4.Силы в зацеплении.

Для определения опорных реакций и изгибающих моментов необходимо составить расчетную схему, основанием которой является эскизная компоновка и схема сил в зацеплении. Опорные реакции определяют, составляя уравнение равновесия в каждой из плоскостей действия сил. В цилиндрической прямозубой передаче силу в зацеплении одной пары зубьев раскладывают на две взаимно перпендикулярные составляющие (рисунок 4,а): окружную силу - F_t и радиальную - F_r. В цилиндрической косозубой передаче силу в зацеплении раскладывают на три составляющие (рисунок 4, б): окружную - F_t, радиальную - F_r и осевую - F_a. Окружная сила на шестерне направлена по касательной к делительному диаметру в противоположном направлении вращения, а для колеса направление окружной силы совпадает с направлением вращения. Радиальные силы направлены по радиусу к центру колес. Радиальная сила  в косозубой цилиндрической передаче направлена по радиусу к центру колеса.

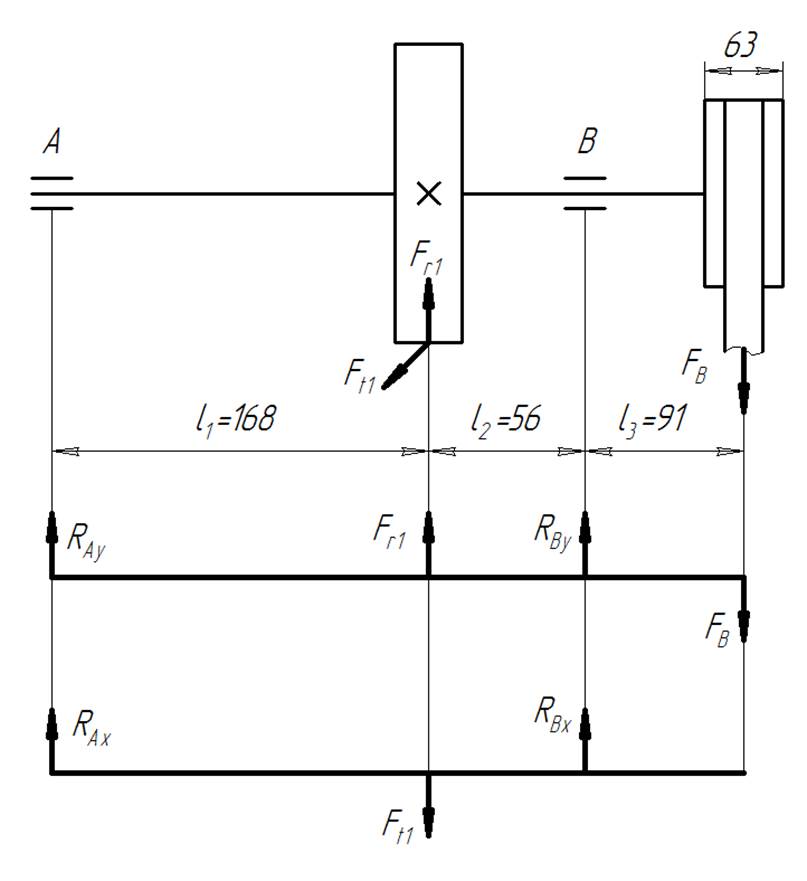
Рисунок 5 – Расчетная схема ведущего вала

Определяем реакции опор в вертикальной плоскости ведущего вала.

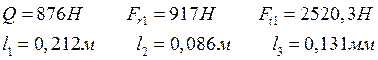
                                                                            (10.1)

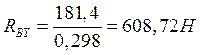
                                              (10.2)

Проверяем правильность решения в вертикальной плоскости вала:

                                                                              (10.3)

Реакции опор найдены верно!

Определяем реакции опор в горизонтальной плоскости ведущего вала:

                                              (10.4)

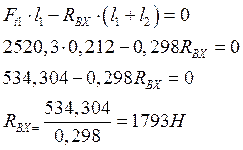
                                              (10.5)

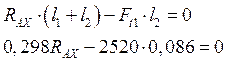
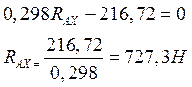
Проверяем правильность решения в горизонтальной плоскости вала:

                                                                             (10.6)

Реакции опор найдены верно!

Определяем суммарные реакции в опорах:

                                                       (10.7)

                                                       (10.8)

                        

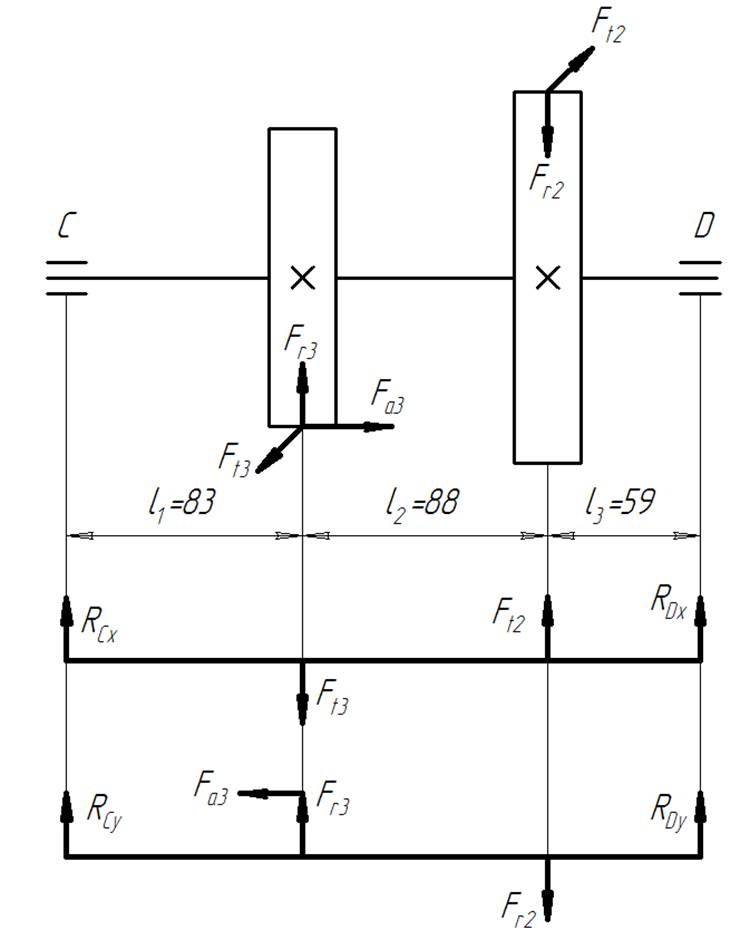
Рисунок 6.Расчетная схема промежуточного вала

Определяем реакции опор в вертикальной плоскости промежуточного вала:

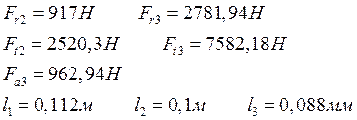
                                               (10.9)

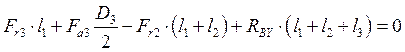
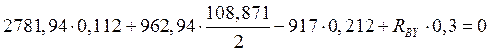
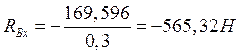
                                              (10.10)

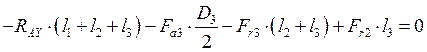
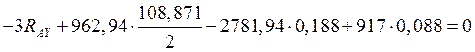
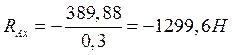
Проверяем правильность решения в вертикальной плоскости вала:

                                                                      (10.11)

Реакции опор найдены верно!

Определяем реакции опор в горизонтальной плоскости промежуточного вала.

                                              (10.12)

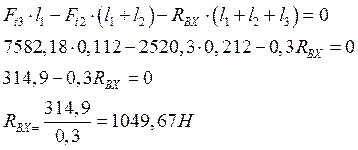
                                              (10.13)

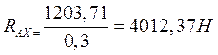
Проверяем правильность решения в горизонтальной плоскости вала:

                                                             (10.14)

Реакции опор найдены верно!

Определяем суммарные реакции в опорах по формуле:

                                                       (10.15)

                                                       (10.16)

                        

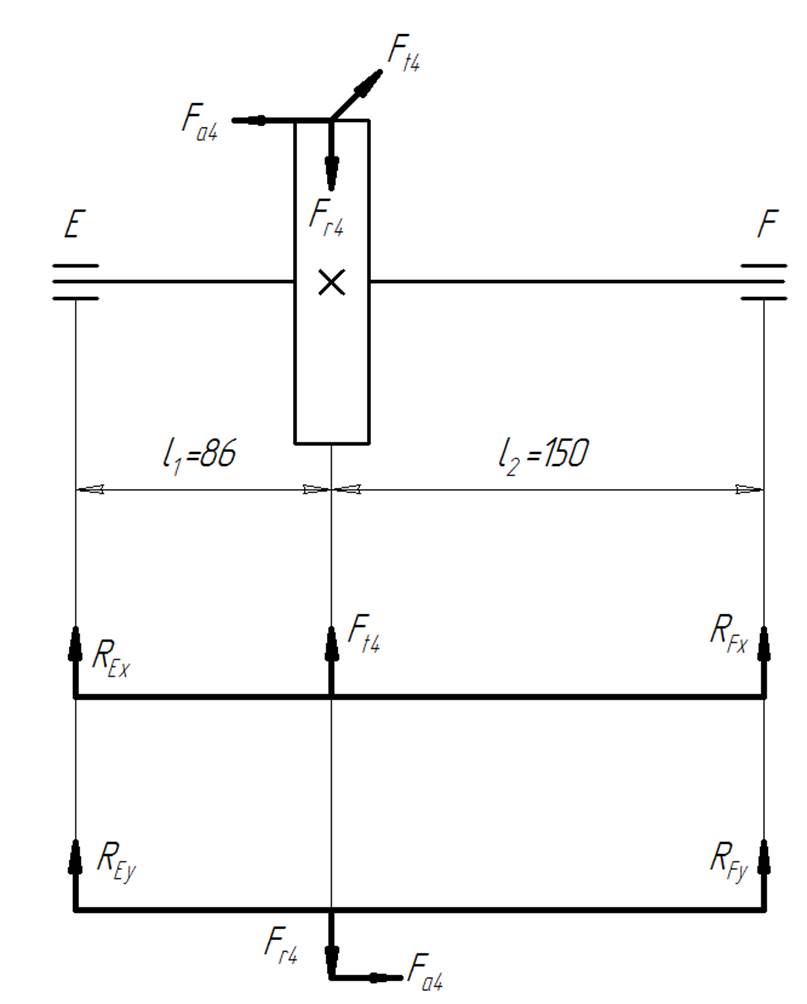
Рисунок 7. Расчетная схема выходного вала

Определяем реакции опор в вертикальной плоскости выходного вала.

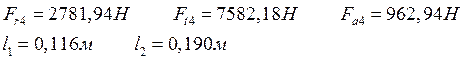
                                                                            (10.17)

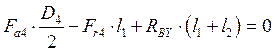
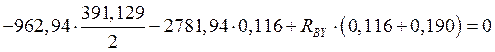
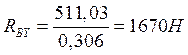
                                              (10.18)

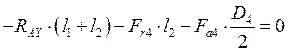
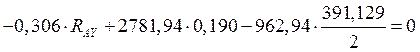
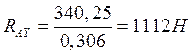
Проверяем правильность решения в вертикальной плоскости вала:

                                                                                 (10.19)

Реакции опор найдены верно!

Определяем реакции опор в горизонтальной плоскости выходного вала.

                                              (10.20)

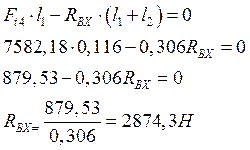
                                              (10.21)

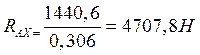
Проверяем правильность решения в горизонтальной плоскости вала:

                                                                                 (10.22)

Реакции опор найдены верно!

Определяем суммарные реакции в опорах:

                                                       (10.23)

                                                       (10.24)

                        

11. Проверочный расчет подшипников

Определяем эквивалентную нагрузку:

,                             (11.1)

где Х – коэффициент радиальной нагрузки, принимаем X=1;

V – коэффициент, учитывающий вращение колец, принимаем V=1,0;

F_{r n} – радиальная нагрузка подшипника;

Y – коэффициент осевой нагрузки;

F_{a n} – осевая нагрузка;

 - коэффициент безопасности, принимаем = 1,2;

 - температурный коэффициент, принимаем = 1,0;

Вал I

Шарикоподшипник № 207

Так как на ведущем валу передача прямозубая, то, следовательно, осевая сила отсутствует.

Принимаем .

Вал II

Шарикоподшипник № 209.

На промежуточном валу передача косозубая, в зацеплении присутствует осевая нагрузка .

В зависимости от отношения , где С₀- статическая грузоподъемность подшипника, определяем коэффициент осевого нагружения по табл. 7.3 [1], где выбираем X и Y.

С₀=17,8 кН.

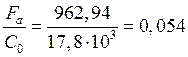, данному значению соответствуют коэффициенты x=0,56; y=1,71.

Для дальнейшего расчета определяем отношение , где -реакция в опоре и -сила в зацеплении, и сравнить его с нормативным значением коэффициента е: если данное отношение больше е, то осевую нагрузку F_a учитываем при определении P_экв , если меньше е, то не учитываем.

Данный расчет ведем для наиболее нагруженной опоры.

Принимаем

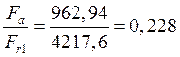<-осевую нагрузкуне учитываем.

Принимаем                 

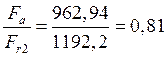>-осевую нагрузку учитываем.

Принимаем .

Вал III

Шарикоподшипник № 215

На выходном валу передача косозубая, в зацеплении присутствует осевая нагрузка .

С₀=41,1 кН.

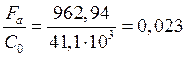, данному значению соответствуют коэффициенты x=0,56; y=1,99.

Для дальнейшего расчета определяем отношение , где -реакция в опоре и -сила в зацеплении, и сравнить его с нормативным значением коэффициента е: если данное отношение больше е, то осевую нагрузку F_a учитываем при определении P_экв , если меньше е, то не учитываем.

Данный расчет ведем для наиболее нагруженной опоры.

Принимаем                 

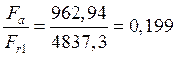<-осевую нагрузкуне учитываем.

Принимаем                 

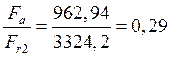>-осевую нагрузку учитываем.

Принимаем .

Определяем расчетную долговечность подшипников по формуле:

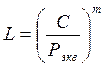                                                (12.1)

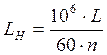                                                (12.2)

где L – долговечность, в млн. об;

L_Н – долговечность, в ч;

С – динамическая грузоподъемность подшипника;

m – коэффициент, равный для шариковых подшипников 3;

n – частота вращения вала;

Вал I

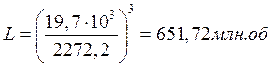
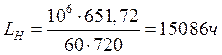
Вал II

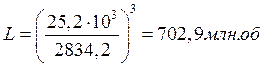
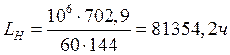
Вал III

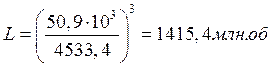
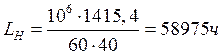
12. Расчет ведомого вала по переменным напряжениям.

 

B

                                                                                                 

A

                                                                

 

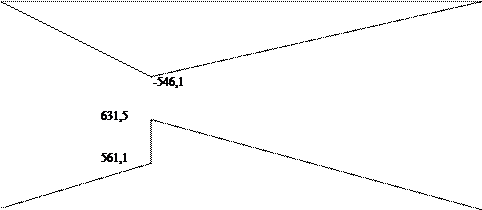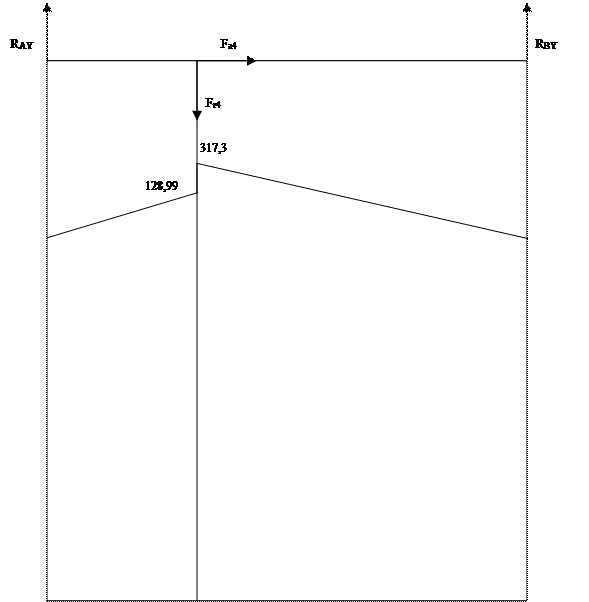
Рисунок 8.Эпюра моментов вычодного вала.

Расчет производим по выходному валу, так как он наиболее нагружен