Техническая характеристика привода. Кинематический расчёт привода. Определение силовых и скоростных параметров передачи

Серии 4А 132S2 с номинальной мощностью 5,5 кВт с асинхронной частотой вращения 970 об/мин.

1.2 Определение общего передаточного числа

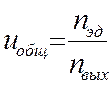                                          (1.3)

где -общее передаточное число привода,

 - частота вращения вала электродвигателя,

 - частота вращения на ведомом валу.

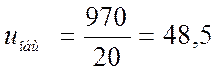
                                           (1.4)

где  - передаточное число конической передачи.

 - передаточное число тихоходной ступени.

-  передаточное число быстроходной ступени.

Принимаем:  = 3,15 ; =3,55 ; =4,34;

и  взяты из стандартного ряда чисел.

рекомендуется принимать равной 4,34

1.3 Определение силовых и скоростных параметров передачи.

Определим частоту вращения ведущего вала

                                (1.5)

 

где n₁-частота вращения ведущего вала.

Определим частоту вращения промежуточного вала

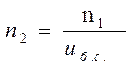                                                  (1.6)        

где - частота вращения промежуточного вала, об/мин.

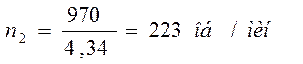
Определим частоту вращения ведомого вала

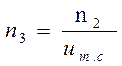                                        (1.7)                                                                                              

где - частота вращения ведомого вала, об/мин.

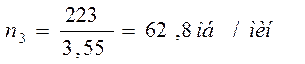
Определим частоту вращения ведомого вала

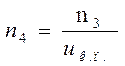                                        (1.8)                                                                                             

где - частота вращения ведомого вала, об/мин.

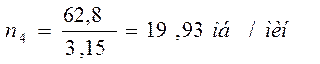
Вычислим отклонение:

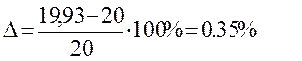
Отклонение не превышает 3%

                    Определяем угловую скорость на валах привода

,                                          

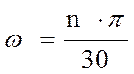Определяем угловую скорость на валу электродвигателя:

                                                                                                    (1.9)                                                                         

где, - угловая скорость вала электродвигателя, с^-1.

Определяем угловую скорость на ведущем валу:

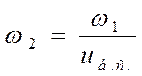
(1.10)           
где ,-угловая скорость ведущего вала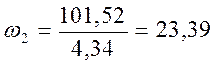, с^-1

 с^-1

Определяем угловую скорость на промежуточном валу:

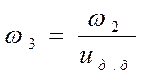                                                                                     (1.11)

где ,-угловая скорость промежуточного  вала, с^-1       

 

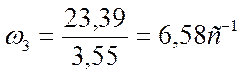
Определяем угловую скорость на ведомом валу:

                                          (1.12)

где, -угловая скорость ведущего вала, с^-1

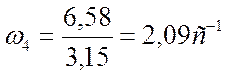
Определение мощности на валах привода

Р₁=P_тр·η_п.п.                                                          (1.13) где, Р₁ – мощность на ведущем валу, кВт.

       Р_тр-  требуемая мощность  электродвигателя, кВт.

                                            Р₁=4,54·0,99=4,49 кВт

                                                 Р₂= Р₁·η_ц.п.·η_п.п.                                                 (1.14)

                                      ,                                                

где ,Р₂ – мощность на промежуточном валу, кВт.

Р₂=4,49·0,98·0,99=4,35 кВт

                                               Р₃= Р₂· η_ц.п· η_п.п.                                                  (1.15)

где ,Р₃ – мощность на ведомом валу.

Р₃=4,35·0,98·0,99=4,22 кВт

                                               Р₄= Р₃· η_к.п· η_п.п.                                                  (1.16)

где ,Р₄ – мощность на ведомом валу.

Р₄=4,22·0,96·0,99=4,01 кВт

          Определяем  вращающие моменты на валах привода

                                             

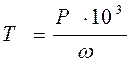
Определяем вращающий момент на валу электродвигателя:

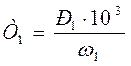                                                   (1.17)

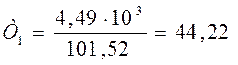 Нм.

Определяем вращающий момент на ведущем валу:

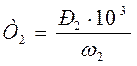                                                                                                   (1.18)

где Т₂ – вращающий  момент на ведущем валу, Нм.

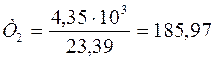Нм

Определяем вращающий момент на промежуточном валу:

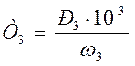                                                      (1.19)

где ,Т₃ – вращающий момент на промежуточном валу, Нм.

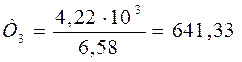Нм

Определяем вращающий момент на ведомом валу:

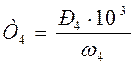,                                                   (1.20)     

где Т₄ – вращающий момент на ведомом валу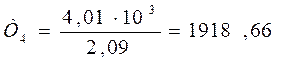, Нм.

Нм  

Табл.2 Силовые и кинематические параметры привода.      

2. Расчет закрытой быстроходной косозубой цилиндрической           передачи

Цель работы: Выбрать материал для быстроходной ступени, рассчитать геометрические параметры, определить силы в зацеплении, проверка передачипоконтактным напряжениям и проверка зубьев на изгиб.

2.1 Выбор материала и определение допускаемых напряжений.

Для шестерни принимаем материал – Сталь 45, с твердостью поверхности зубьев НВ₁=230, достигаемое термообработкой – улучшением.

Для колеса принимаем материал – Сталь 45, с твердостью поверхности зубьев НВ₂=180, достигаемое термообработкой – улучшением.

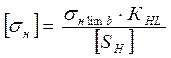 ,                                                (2.1)

где -  допускаемые  контактные напряжения для материала шестерни и колеса  Н/мм².

- предел контактной выносливости при базовом числе циклов.

 - коэффициент долговечности при контактных деформациях.

Принимаем =1

[S] =1,1 – коэффициент безопасности.

Для шестерни: σ_нlimb=2·230+70=530 мПа.

Для колеса: σ_нlimb=2·180+70=430 мПа.

Для шестерни:

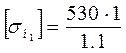=481,8 мПа.

Для колеса:

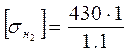=390,9 мПа.

Расчетное допускаемое контактное напряжение для косозубых колес:

2.2 Геометрический расчет передачи.

 Определяем межосевое расстояние передачи:

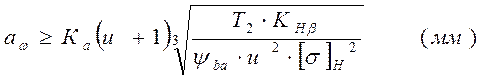           (2.2)

где  - межосевое расстояние, мм.

К _a– постоянное число.

u– передаточное числобыстроходной передачи .

T₂ – вращающий момент на валу колеса, Нм.

- коэффициент неравномерного распределения нагрузки по ширине зубчатого колеса.

 - коэффициент ширины  венца.

Принимаем =0,4; К=43; =1,2.

мм

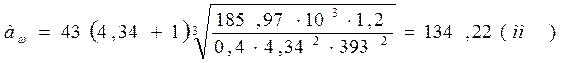
Принимаем по ГОСТу = 140  мм.

Расчет модуля зацепления:

                                                                                                  (2.3)

мм.

По ГОСТ 9563 – 60  принимаем стандартное значение m=2мм. 

Примем предварительно угол наклона зубьев β=10° и определим числа зубьев шестерни и колеса.

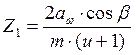,                                               (2.4)

где Z₁ –число зубьев шестерни.

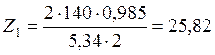
Принимаем Z₁ = 26.

Тогда:  Z₂=Z₁·u=26·4,34=112,84

          Принимаем z₂=113

Уточняем передаточное число:

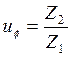,                                                    (2.5)

где u_ф – фактическое передаточное число.

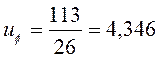
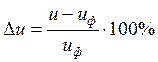                                            (2.6)      

 

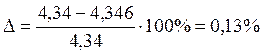
0,13% < 3%  допустимо

Уточненное значение угла наклона зубьев:

cosβ=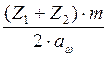                                    (2.7) 

cosβ=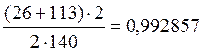

β=7°25'

Определение геометрических размеров шестерни и колеса:

Определяем делительные диаметры шестерни и колеса:

 ,                                                      (2.8)

 ,                                                     (2.9)

где d_1,2– делительный диаметр, мм

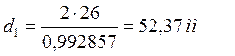
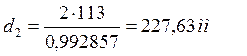
Проверка:

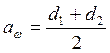                                                  , мм                                                (2.10)

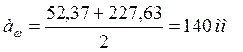
Определяем диаметры вершин зубьев:

                                                  ,                                            (2.11)        

,                                            (2.12)    

где d_а1,а2 – диаметры вершин зубьев, мм.

Определяем диаметры впадин:

                                      (2.13)

                           (2.14)                                                                                                                                   

где d_fi,f2 – диаметры впадин, мм

мм

мм

Определяем ширину колеса:

                                                    (2.15)

Определяем ширину шестерни:               

                                                   (2.16)                                              

где: b_1,2 – ширина венцов, мм.

мм

мм

Определяем коэффициент ширины шестерни по диаметру:

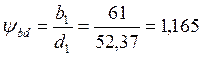
Окружная скорость колес и степень точности передачи:

,                                                 (2.17)       где V – окружная скорость, м/c.

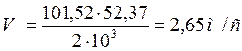
При  такой скорости для косозубых колёс  следует принять 8-ю степень точности .

Коэффициент нагрузки:

K_H=K_Hβ·K_Hά·K_HV                                                                                                                             (2.18)

При ψ_bd=1,2,твёрдости HB≤350 и несимметричном расположении колёс относительно опор K_Hβ=1,15.

При V=1,26м/с и 8-й степени точности  K_Hά=1,06.

Для косозубых колёс при V≤5м/с имеем K_Hv=1.

K_H=1,15·1,06·1=1,219

Проверка контактных напряжений по формуле:

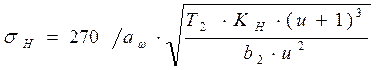
(2.19)

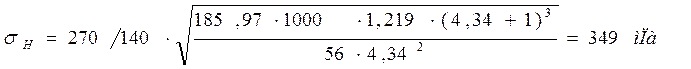
σ_H=349мПа<[ σ_H]=393мПа.

Δ=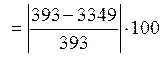%=11%<10%-перегруз

Так как напряжения превысили допускаемую норму 10%,тогда уменьшаем ширину колеса до 50мм.

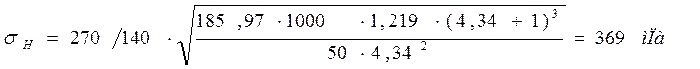
Δ=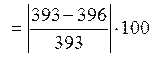%=6,1%<10%-недогрузка в пределах нормы.

2.3 Силы в зацеплении.

Окружная сила : 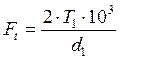                              (2.20)

где, F_t- окружная сила в зацеплении, Н  

       T₁ – вращающий момент на валу колеса.

d₁ – делительный диаметр колеса.

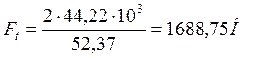
Радиальная сила :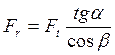                                                             (2.21)

где α - угол зацепления в нормальном сечении.

β – угол наклона зубьев.

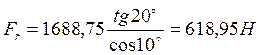
                Осевая сила :                                                                  (2.22)

2.4 Проверочный расчёт зубьев на выносливость по напряжениям изгиба.

Ппроверяем зубья на выносливость по напряжениям изгиба по формуле:

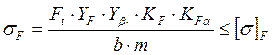                                           (2.23)

Здесь коэффициент нагрузки K_F=K_Fβ·K_FV                                                       (2.24)

При ψ_bd=1,165,твёрдости HB<350 и несимметричном расположении зубчатых колёс относительно опор K_Fβ=1,13; K_FV=1,1.

K_F=1,13·1,1=1,243.

Y_F-коэффициент,учитывающий форму зуба и зависящий от эквивалентного числа зубьев Z_v:

Для шестерни: 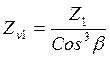  ,                                                                    (2.25)

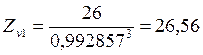, принимаем Z_V1=27;

Для колеса:        ,                                                                     (2.26)

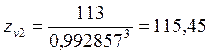, принимаем Z_V2=116;

Y_F1=3,90 и Y_F2=3,60.

Допускаемое напряжение определяется по формуле:

[σ_F]= 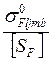                               (2.27)

Для стали 45 улучшенной при твёрдости HB<350   σ_Flimb =1,8HB.

Шестерня: σ_Flimb =1,8·230=415мПа.

Колесо: σ_Flimb =1,8·180=324мПа.

[S_F]= [S_F]^’·[S_F]^’’-коэффициент безопасности.                                         (2.28)

[S_F]^’=1,75 и [S_F]^’’=1-для поковок.

[S_F]=1,75·1=1,75.

Допускаемые напряжения:

[σ_F1]=

[σ_F2]=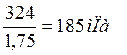

Находим отношения 

Шестерня: 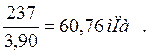;  Колесо: ;

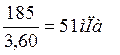Определяем коэффициенты Y_β и K_Fά:

                                                          ,                                              (2.29)

Y_β – коэффициент учитывающий наклон зуба.

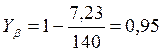
K_Fά=0,92.

Проводим проверочный расчет зубьев на изгиб.

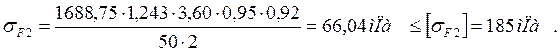
Вывод:Условие прочности выполнено.

3. Расчет закрытой тихоходной косозубой цилиндрической           передачи

Цель работы: Выбрать материал для быстроходной ступени, рассчитать геометрические параметры, определить силы в зацеплении, проверка передачипоконтактным напряжениям и проверка зубьев на изгиб.

3.1 Выбор материала и определение допускаемых напряжений.

Для шестерни принимаем материал – Сталь 45, с твердостью поверхности зубьев НВ₁=280, достигаемое термообработкой – улучшением.

Для колеса принимаем материал – Сталь 45, с твердостью поверхности зубьев НВ₂=230, достигаемое термообработкой – улучшением.

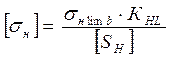 ,                                                (3.1)

где -  допускаемые  контактные напряжения для материала шестерни и колеса  Н/мм².

- предел контактной выносливости при базовом числе циклов.

 - коэффициент долговечности при контактных деформациях.

Принимаем =1

[S] =1,1 – коэффициент безопасности.

Для шестерни: σ_нlimb=2·280+70=630 мПа.

Для колеса: σ_нlimb=2·230+70=530 мПа.

Для шестерни:

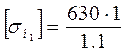=572,72 мПа.

Для колеса:

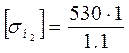=481,8 мПа.

Расчетное допускаемое контактное напряжение для косозубых колес:

2.2 Геометрический расчет передачи.

 Определяем межосевое расстояние передачи:

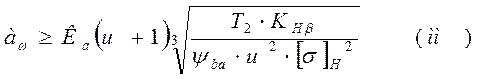            (3.2)

где  - межосевое расстояние, мм.

К _a– постоянное число.

u– передаточное числобыстроходной передачи .

T₂ – вращающий момент на валу колеса, Нм.

- коэффициент неравномерного распределения нагрузки по ширине зубчатого колеса.

 - коэффициент ширины  венца.

Принимаем =0,4; К=43; =1,2.

мм

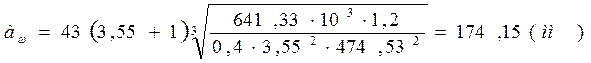
Принимаем по ГОСТу = 180  мм.

Расчет модуля зацепления:

                                                                                                  (3.3)

мм.

По ГОСТ 9563 – 60  принимаем стандартное значение m=2,5мм. 

Примем предварительно угол наклона зубьев β=10° и определим числа зубьев шестерни и колеса.

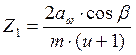,                                               (3.4)

где Z₁ –число зубьев шестерни.

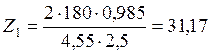
Принимаем Z₁ = 31.

Тогда:  Z₂=Z₁·u=31·3,55=110,05

          Принимаем z₂=110

Уточняем передаточное число:

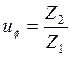,                                                    (3.5)

где u_ф – фактическое передаточное число.

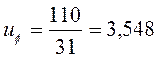
                                            (3.6)      

 

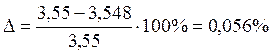
0,056% < 3%  допустимо

Уточненное значение угла наклона зубьев:

cosβ=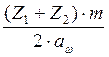                                    (3.7) 

cosβ=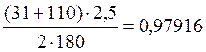

β=11°71'

Определение геометрических размеров шестерни и колеса:

Определяем делительные диаметры шестерни и колеса:

 ,                                                      (3.8)

 ,                                                     (3.9)

где d_1,2– делительный диаметр, мм

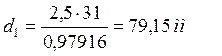
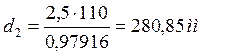
Проверка:

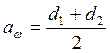                                                  , мм                                                (3.10)

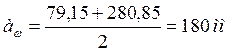
Определяем диаметры вершин зубьев:

 ,                                            (3.11)        

,                                            (3.12)    

где d_а1,а2 – диаметры вершин зубьев, мм.

Определяем диаметры впадин:

                                      (3.13)

                           (3.14)                                                                                                                                   

где d_fi,f2 – диаметры впадин, мм

мм

мм

Определяем ширину колеса:

                                                    (3.15)

Определяем ширину шестерни:               

                                                   (3.16)                                              

где: b_1,2 – ширина венцов, мм.

мм

мм

Определяем коэффициент ширины шестерни по диаметру:

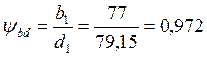
Окружная скорость колес и степень точности передачи:

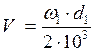,                                                 (3.17)       где V – окружная скорость, м/c.

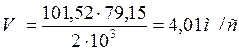
При  такой скорости для косозубых колёс  следует принять 8-ю степень точности .

Коэффициент нагрузки:

K_H=K_Hβ·K_Hά·K_HV                                                                                                                          (3.18)

При ψ_bd=1,2,твёрдости HB≤350 и несимметричном расположении колёс относительно опор K_Hβ=1,15.

При V=1,26м/с и 8-й степени точности  K_Hά=1,06.

Для косозубых колёс при V≤5м/с имеем K_Hv=1.

K_H=1,15·1,06·1=1,219

Проверка контактных напряжений по формуле:

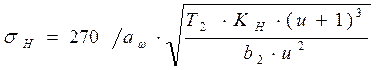
(3.19)

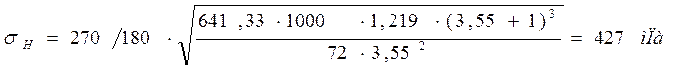
σ_H=427мПа<[ σ_H]=474мПа.

Δ=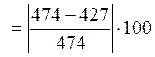%=9,91%<10%- недогрузка в пределах нормы.

2.3 Силы в зацеплении.

Окружная сила : 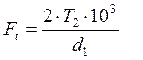                              (3.20)

где, F_t- окружная сила в зацеплении, Н  

T₁ – вращающий момент на валу колеса.

d₁ – делительный диаметр колеса.

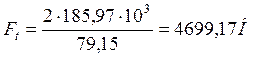
Радиальная сила :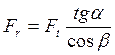                                                             (3.21)

где α - угол зацепления в нормальном сечении.

β – угол наклона зубьев.

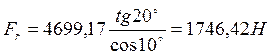
                Осевая сила :                                                                  (3.22)

2.4 Проверочный расчёт зубьев на выносливость по напряжениям изгиба.

Ппроверяем зубья на выносливость по напряжениям изгиба по формуле: