3. Построение плана положений механизма
Построим план положений механизма для одного цикла его движения. Под циклом для заданного механизма принимается полный оборот кривошипа.
Для этого сначала определим масштаб
плана положений ![]() по формуле:
по формуле: 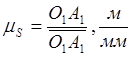 , где
, где ![]() -
истинная длина кривошипа, м;
-
истинная длина кривошипа, м; ![]() - чёртёжное
изображение длины кривошипа, мм.
- чёртёжное
изображение длины кривошипа, мм.
Произвольно примем, что чёртёжное
изображение длины кривошипа ![]() равно
равно ![]() . Отсюда получим:
. Отсюда получим: 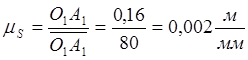 .
.
В принятом масштабе чертёжные
изображения остальных звеньев механизма равны: 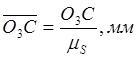 ,
,
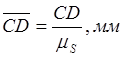 ,
, 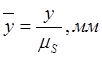 ,
,
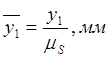 , где
, где ![]() - чёртёжное изображение длины звена
- чёртёжное изображение длины звена ![]() , мм;
, мм; ![]() -
истинная длина данного звена, м;
-
истинная длина данного звена, м; ![]() - истинная длина
данного звена, м;
- истинная длина
данного звена, м; ![]() - масштаб плана положений,
м/мм; и т.д.
- масштаб плана положений,
м/мм; и т.д.
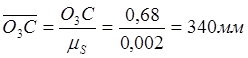
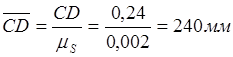
Результаты вычислений чертёжных изображений остальных звеньев механизма приведены в таблице 5.
|
|
|
|
|
|
|
|
80 |
340 |
120 |
185 |
140 |
4. Построение плана скоростей механизма
Построим план скоростей механизма для определения линейных скоростей всех характерных подвижных точек звеньев механизма.
План скоростей механизма строится по структурным группам Л.В. Ассура в порядке их присоединения к начальному механизму.
Для построения плана скоростей
механизма необходимо сначала определить масштаб плана скоростей ![]() по формуле:
по формуле: 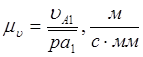 ,
где
,
где ![]() - истинное численное значение
скорости
- истинное численное значение
скорости ![]() , м/c;
, м/c; ![]() - чёртёжное изображение вектора
- чёртёжное изображение вектора ![]() , мм.
, мм.
Рассчитаем истинное численное значение
скорости ![]() :
: 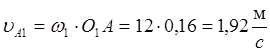 .
Произвольно примем, что чёртёжное изображение вектора
.
Произвольно примем, что чёртёжное изображение вектора ![]() ,
равно
,
равно ![]() . Отсюда получим:
. Отсюда получим: 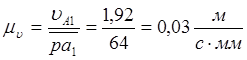 .
.
Построить план скоростей механизма - это значит графически решить векторные уравнения, описывающие характер движения звеньев механизма. Составим эти векторные уравнения для данного механизма перемещения резца.
При рассмотрении движения шатуна 3
движение точки В принадлежащей шатуну, может быть представлено как
переносное вместе с точкой А, принадлежащей кривошипу 1, и как относительное
движение точки В шатуна относительно точки А, а также как
переносное вместе с точкой О3 и как относительное движение
относительно О3. В результате получим систему уравнений 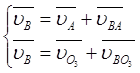 .
.
Решив графически эти векторные
уравнения мы найдем полную скорость точки В. Далее нам необходимо определить
скорость точки D. При рассмотрении движения кулисного
камня 4 вместе с ползуном 5 в данный момент времени получим: ![]() . При рассмотрении движения кулисного
камня 4 вместе с кулисой 2 сложное движение точки
. При рассмотрении движения кулисного
камня 4 вместе с кулисой 2 сложное движение точки ![]() ,
принадлежащей кулисе, может быть представлено как переносное вместе с точкой
,
принадлежащей кулисе, может быть представлено как переносное вместе с точкой ![]() , принадлежащей кулисному камню, и
как относительное движение точки
, принадлежащей кулисному камню, и
как относительное движение точки ![]() кулисы
относительно точки
кулисы
относительно точки ![]() кулисного камня. В
результате получим
кулисного камня. В
результате получим ![]() . При рассмотрении движения
точки
. При рассмотрении движения
точки ![]() только с кулисой 3 в данный момент
времени получим
только с кулисой 3 в данный момент
времени получим ![]() . Решив последовательно эти
векторные уравнения, мы найдём полную скорость точки
. Решив последовательно эти
векторные уравнения, мы найдём полную скорость точки ![]() ,
принадлежащей кулисе. Для нахождения скорости точки
,
принадлежащей кулисе. Для нахождения скорости точки ![]() ,
принадлежащей кулисе воспользуемся свойством пропорции, которое можно записать
в виде:
,
принадлежащей кулисе воспользуемся свойством пропорции, которое можно записать
в виде: 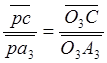 . Таким образом,
. Таким образом, 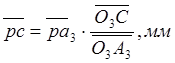 , где
, где ![]() -
чертёжные изображения на плане скоростей векторов
-
чертёжные изображения на плане скоростей векторов ![]() и
и
![]() соответственно, мм;
соответственно, мм; ![]() - чертёжные изображения на плане
положений звеньев механизма
- чертёжные изображения на плане
положений звеньев механизма ![]() и
и ![]() соответственно, мм.
соответственно, мм.
Например, для первого положения
механизма отрезок ![]() находится следующим
образом
находится следующим
образом 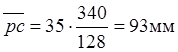 .
.
указать направления векторов их линейных скоростей.
В дальнейшем, основываясь на построенных планах скоростей, необходимо вычислить линейные скорости характерных подвижных точек звеньев механизма по формулам:
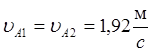 ,
, 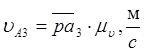 ,
,
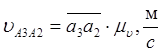 ,
,
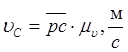 ,
, 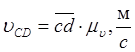 ,
,
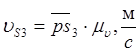 , .
, .
где ![]() - масштаб плана скоростей,
- масштаб плана скоростей, 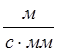 ;
; ![]() -
чёртёжные изображения на плане скоростей векторов
-
чёртёжные изображения на плане скоростей векторов ![]() соответственно,
мм.
соответственно,
мм.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.