 |
По дисциплине: Основы научных исследований
2006
Цель работы:отыскание экстремума функции одной переменной аналитическим путем и одним из численных методов.
Общие сведения:
Задается следующая функция, экстремум которой требуется определить:
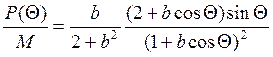 , где
, где 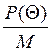 – «приведенное» давление в масляном
клине подшипника мельницы;
– «приведенное» давление в масляном
клине подшипника мельницы;
b – относительный эксцентриситет подшипника;
![]() – угловая координата
эпюры давления.
– угловая координата
эпюры давления.
Решение:
Находим экстремум функции, решая уравнение: 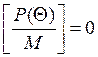
Выведем производную функции:
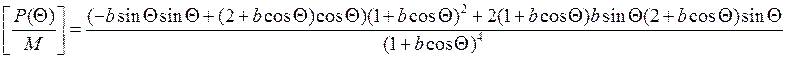
Упростим выражение:
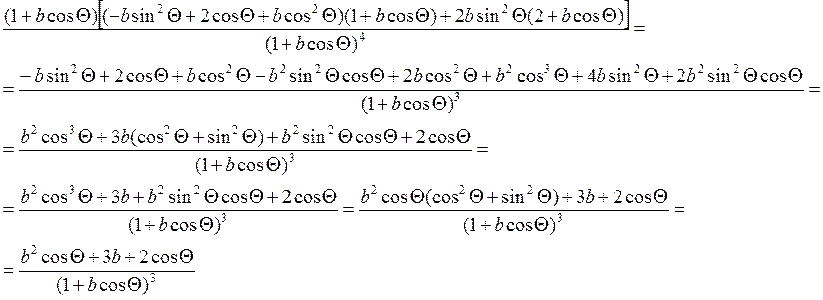
Решаем уравнение и находим экстремум функции:
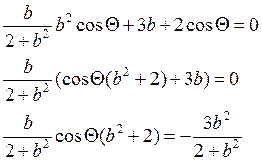
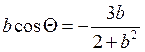
При
![]() получаем уравнение:
получаем уравнение:
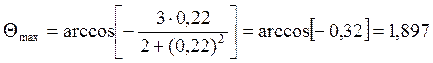
Расчет и построение эпюры приведенного давления
По заданному значению b рассчитываем и строим эпюру приведенного давления с учетом координат экстремума. Расчет производился с применением электронных таблиц Excel 2002. Результаты вычислений заносим в таблицу 1.
Таблица 1
|
№ пп |
|
|
|
|
1 |
0 |
0,000 |
0,000 |
|
2 |
10 |
0,175 |
0,028 |
|
3 |
20 |
0,349 |
0,056 |
|
4 |
30 |
0,524 |
0,083 |
|
5 |
40 |
0,698 |
0,110 |
|
6 |
50 |
0,873 |
0,135 |
|
7 |
60 |
1,047 |
0,159 |
|
8 |
70 |
1,222 |
0,181 |
|
9 |
80 |
1,396 |
0,200 |
|
10 |
90 |
1,571 |
0,215 |
|
11 |
100 |
1,745 |
0,224 |
|
12 |
110 |
1,920 |
0,227 |
|
13 |
120 |
2,094 |
0,222 |
|
14 |
130 |
2,269 |
0,207 |
|
15 |
140 |
2,443 |
0,183 |
|
16 |
150 |
2,618 |
0,148 |
|
17 |
160 |
2,792 |
0,105 |
|
18 |
170 |
2,967 |
0,054 |
|
19 |
180 |
3,142 |
0,000 |
Эпюра представлена на рис.1.
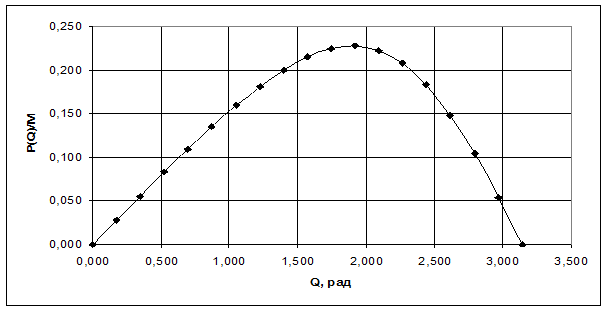
Рис.1 Эпюра приведенного давления в масляном клине
2. Отыскание экстремума функции одной переменной методом поразрядного приближения.
Общие сведения:
Задача поиска экстремума некоторой целевой функции y = F(x) сводится к нахождению интервала [a;b], в котором находится экстремум, и к его сужению. Будем искать максимум F(x). Поскольку при однократном прохождении экстремума (х меняется с шагом Dх), знак приращения F(x) может не изменяться (см. рисунок 2), следует перед дроблением Dх предусмотреть возврат на два шага после изменения знака приращения F(x).
![]()
![]()

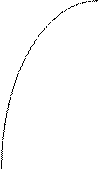
![]() Y=F(x)
Y=F(x)
![]()
![]() x
x
x0 x1 x2 xmax x3 x4 x5
|
ΔQ = 10°; ε = 0,01; ΔY = Yn+1-Yn; ΔY > ε
Расчет производился с применением электронных таблиц Excel 2002. Результаты вычислений заносим в таблицу 2.
|
№ пп |
x, град |
Y |
|
1 |
0 |
0,000 |
|
2 |
10 |
0,028 |
|
3 |
20 |
0,056 |
|
4 |
30 |
0,083 |
|
5 |
40 |
0,110 |
|
6 |
50 |
0,135 |
|
7 |
60 |
0,159 |
|
8 |
70 |
0,181 |
|
9 |
80 |
0,200 |
|
10 |
90 |
0,215 |
|
11 |
100 |
0,224 |
|
12 |
110 |
0,227 |
|
13 |
120 |
0,222 |
|
14 |
130 |
0,207 |
|
15 |
140 |
0,183 |
|
16 |
150 |
0,148 |
|
17 |
160 |
0,105 |
|
18 |
170 |
0,054 |
|
19 |
180 |
0,000 |
Из таблицы видим, что ΔY = Yn+1 – Yn = Y12 – Y11 = 0,227–0,224 = 0,03
ΔY = Yn+1–Yn = Y13–Y12 = 0,222–0,227 = -0,05
Ymax= 0,227 – экстремум функции.
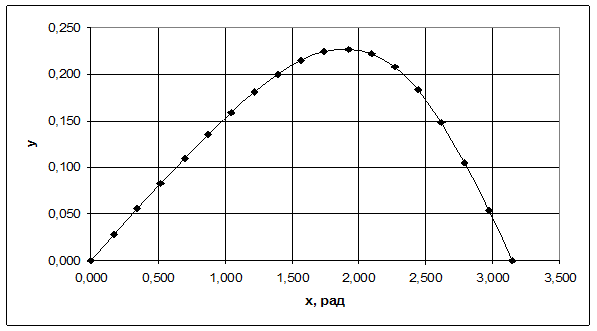
Рис.3. Поиск экстремума функции методом поразрядного приближения
Вывод: Данная методика позволяет найти экстремум функции, который в свою очередь является (в данном случае) оптимальным давлением подачи масла в клин подшипника.
Контрольные вопросы
1. Какие вы знаете способы поиска экстремума для недифференцированных функций?
– Нахождение экстремума функции заданной аналитическим выражением;
– Отыскание экстремума функции одной переменной методом поразрядного приближения.
2. В чем суть градиентного метода?
Основная идея метода состоит в том, чтобы двигаться к минимуму в направлении наиболее быстрого убывания функции, который определяется антиградиентом.
3. Охарактеризуйте методы покоординатного спуска и наискорейшего спуска.
С помощью метода покоординатного спуска мы построим последовательность точек М0, М1, М2 и т.д. и которой соответствует монотонная последовательность значений функции f(M0)≥f(M1) ≥f(M2) и т.д. Отрывая этот процесс на некотором шаге К, можно приблизительно принять за оптимум значения функции на этом шаге f(MK).
Согласно методу наискорейшего спуска после вычитания в начальной точке градиента функции делают в направлении антиградиента не маленький шаг, а движется до тех пор пока функция убывает. Достигнув точки минимума на выбранном направлении, снова вычисляют градиент функции и повторяют описанную процедуру. При этом градиент вычисляется гораздо реже, только при смене направления движения. Хотя траектория ведет к цели не так быстро, как в случае градиентного спуска, экономия машинного времени, за счет более редкого вычисления градиента, может быть весьма существенной.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.