 |
По дисциплине: Основы научных исследований
2004
АППРОКСИМАЦИЯ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ ПО МЕТОДУ НАИМЕНБШИХ КВАДРАТОВ
Цель работы: научиться по заданному классу функций аппроксимировать экспериментальные данные методом наименьших квадратов.
Используемое оборудование: персональный компьютер или инженерный микрокалькулятор.
Общие сведения
Для аппроксимации по методу МНК линейной
зависимости ![]() (т.е. нахождения
коэффициентов
(т.е. нахождения
коэффициентов ![]() и
и ![]() необходимо решить
систему так называемых нормальных уравнений):
необходимо решить
систему так называемых нормальных уравнений):
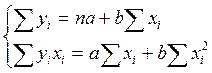
В данной работе необходимо будет научиться аппроксимировать экспериментальную выборку данных тем или иным видом функций (полиномом, экспоненциальной, показательной и др.).
ИСХОДНЫЕ ДАННЫЕ
![]()
|
|
1 |
2 |
2,5 |
3 |
3,5 |
|
|
2 |
8 |
13 |
17 |
25 |
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Линеаризуем выражение ![]() . Для этого прологарифмируем
левую и правую части уравнения:
. Для этого прологарифмируем
левую и правую части уравнения:
![]() .
.
2. Составим систему нормальных уравнений:
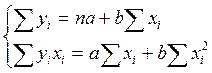
Тогда получим расчётную систему уравнений.
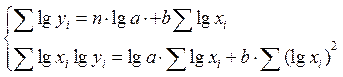
3. Для удобства решения системы уравнений составим вспомогательную табл.1.
Таблица 1
|
Вспомогательные числа |
Суммы |
|||||
|
|
1 |
2 |
2,5 |
3 |
3,5 |
12 |
|
|
0 |
0,3 |
0,4 |
0,48 |
0,54 |
1,72 |
|
|
0 |
0,09 |
0,16 |
0,23 |
0,29 |
0,77 |
|
|
2 |
8 |
13 |
17 |
25 |
– |
|
|
0,3 |
0,9 |
1,11 |
1,23 |
1,4 |
4,94 |
|
|
0 |
0,27 |
0,44 |
0,59 |
0,76 |
2,06 |
4. Решим систему уравнений, подставим найденные значения из вспомогательной таблицы:
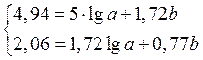
Для упрощения записей введём некоторые обозначения:
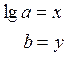
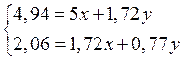
Из первого уравнения выразим x:
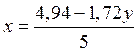
Подставив ![]() во
второе уравнение, получим:
во
второе уравнение, получим:
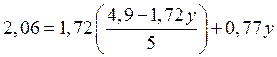
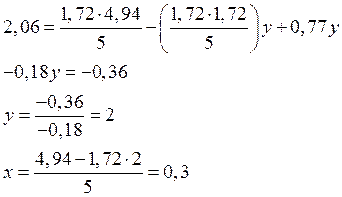
Так как мы приняли ![]() и
и
![]() , то
, то ![]() и
и ![]() будут следующие:
будут следующие:
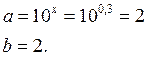
5. После вычислений методом наименьших квадратов заданное уравнение будет выглядеть следующим образом:
![]()
6. Сделаем проверку. Подставим в уравнение ![]() иксы, чтобы полученные по
этому уравнению игреки сравнить с исходными из таблицы задания:
иксы, чтобы полученные по
этому уравнению игреки сравнить с исходными из таблицы задания:
|
xi |
1 |
2 |
2,5 |
3 |
3,5 |
|
yi по условию |
2 |
8 |
13 |
17 |
25 |
|
yi по уравне-нию y=2x2 |
2 |
8 |
12,5 |
18 |
24,5 |
7. Вывод: Учитывая близкую сходимость результатов, можно утверждать, что аппроксимируемая функция адекватна реальному проекту.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.