Расчет зубчатой цилиндрической передачи редуктора, (тихоходная ступень). Условие прочности по напряжениям изгиба

З. Расчет зубчатой цилиндрической передачи редуктора.

(тихоходная ступень)

Для изготовления шестерни применяем сталь 40Ч с термообработкой – поверхностная закалка с нагревом ТВЧ до твердости HRC 45…50, HRC_ср = 47,5, для изготовления зубчатого колеса применим сталь 40ХН улучшенную с твердостью НВ 269…302, НВ_ср = 285,5, =690 МПа. [3. стр. 34].

Допускаемые контактные напряжения:

Мпа;                           (3.1)

где: - предел контактной выносливости при базовом числе циклов.

Для стали 40Х с твердостью НКС 45…50:

= 17·HRC + 200 = 17 · 47,5 + 200 = 1007,5 МПа [3. стр. 34];

Для стали 40 ХН улучшенной:

= 2·HВ + 70 = 2 ·285,5 + 70 = 641 МПа [3. стр. 34];

k_HL – коэффициент долговечности [1. стр. 33].

                                           (3.2)

N_HO – базовое число циклов перемены напряжений, соответствующее пределу выносливости:

для шестерни HRC47,5 ~ HB 488:

N_HO3 = HB³ =  488³ = 1,16 · 10⁸ циклов.

Для колеса:

N_HO4 = HB³ =  285,5³ = 2,3 · 10⁷ циклов.

N_НЕ – число циклов перемены напряжений за весь срок службы:

                                    (3.3)

для шестерни:

N_НЕ3 = 60 · 145,5 · · 0,3 · 7008 + 0,25³ · 0,7 · 7008 = 1,9 · 10⁷ циклов.

Для колеса:

N_НЕ4 =  циклов.             (3.4)

Тогда:

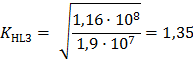
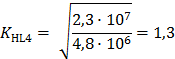
 - коэффициент безопасности.

Для колес из улучшенной стали   =1,1…1,2 [3. стр. 33].

Для шестерни с поверхностной закалкой ТВЦ  = 1,2…1,3.

МПа;

МПа;

Для не прямозубых колес рассчитанное допустимое контактное  напряжение [3.стр.35]:

                                   (3.5)

МПа

Требуемое условие - выполнено.

Допускаемое напряжение изгиба [3.стр.44]:

                            (3.6)

где:  - предел выносливости при эквивалентном числе циклов;

                      (3.7)

Для материала шестерни:

 = 700 МПа [3. стр. 44]

Для колеса:

 = 1,8 НВ = 1,8 · 285,5 = 514 МПа [3. стр. 44]      (3.8)

k_Fg – коэффициент, учитывающий шлифования переходной поверхности зубьев, при отсутствии шлифования k_Fg = 1,0 [3. стр. 44];

k_Fd – коэффициент, учитывающий влияние деформационного упрочнения или электрохимической обработки переходной поверхности; при отсутствии такого упрочнения k_Fd = 1,0;

k_Fс – коэффициент, учитывающий влияние двухстороннего приложения нагрузки; при одностороннем приложении нагрузки k_Fс = 1,0;

k_FL – коэффициент долговечности;

Поскольку для всех сталей ГОСТ принимаем базовое число циклов                 N_FO = 4 · 10⁶, то:                                                ;                                (3.9)

m_F = 6 при твердости зубьев НВ < 350;

m_F = 9 при твердости зубьев НВ > 350;

N_FE – эквивалентное число циклов:

                                     (3.10)

для шестерни:

N_FE3 = 60 · 36,4 · Σ1⁹ · 0,3 · 7008 + 0,25⁹ · 0,7 · 7008 = 1,8 · 10⁷циклов для колеса:

N_FE4 = 60 · 36,4 · Σ1⁶ · 0,3 · 7008 + 0,25⁶ · 0,7 · 7008 = 4,6 · 10⁶циклов

Так как:                                 N_FE3>4·10⁶ и N_FE4>4·10⁶

То:                                                K_FL3 = K_F4 = 1,0

= 700 · 1,0 · 1,0 · 1,0 · 1,0 = 700 МПа;

= 514 · 1,0 · 1,0 · 1,0 · 1,0 = 514 МПа.

Y_S – коэффициент, учитывающий градиент напряжений, зависящий от модуля; при значении модуля от 1 до 8 мм Y_S = 1,1…0,92 [3.стр.46].

Y_R – коэффициент, учитывающий шероховатость переходной поверхности; он отличен от 1,0 в случае полирования;

k_XF – коэффициент, учитывающий размеры колеса; при d_a ≤ 300 vv k_XF = -1,0 [3. Стр.46].

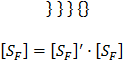 [3.стр.44]                    (3.11)

- коэффициент, учитывающий нестабильность свойств материала; для материала шестерни и материала колеса =1,75 [3.стр.45].

- коэффициент, учитывающий способ получения заготовки; для наковок и штамповок = 1,0 [3.стр.44].

для шестерни:

для колеса:

.

Межосевое расстояние из условия контактной выносливости:

мм                   (3.12)

где:   k_a = 43 – для косозубой передачи;

k_Нβ – коэффициент нагрузки; при несимметричном расположении зубчатого колеса. Предварительно принимаем k_Нβ = 1,25 [3.стр.32].

ψ_ва – коэффициент ширины венца по межосевому расстоянию; для косозубых колес принимаем ψ_ва = 0,4.

мм

Ближайшее значение межосевого расстояния по СТСЭВ 229-75 а_W = 160 мм.

Нормальный модуль зацепления m_п = (0,01…0,02)а_w = (0,01…0,02)160-1,0…3,2. По СТСЭВ 310-76 принимаем m_п = 3 мм.

Примем предварительно угол наклона зубьев β = 10^о и определим числа зубьев шестерни и колеса:

                 (3.13)

Z₄=Z₃ · U_ц = 21 · 4 = 84.

Уточняем значение угла наклона зубьев:

             (3.14)

β = 10,13^о = 10^о8’.

Основные размеры шестерни и колеса:

Диаметры делительные окружностей:

мм                         (3.15)

мм                      (3.16)

Проверка:

мм                     (3.17)                                         

Диаметры вершин зубьев:

d_a3 = d₃ · 2m_п = 64 + 2 · 3 = 70 мм                    (3.18)

d_a4 = d₄ · 2m_п = 256 + 2 · 3 = 70 мм                   (3.18)

Ширина колеса:

= 0,4 · 160 = 64мм                   (3.19)

Ширина шестерни:

= 64 + 5 = 69мм                   (3.20)

Коэффициент ширины шестерни по диаметру:

                         (3.21)

Окружная скорость колеса:

м/с                 (3.22)

При данной скорости принмаем 8-ю степень точности [3.стр.32].

Определяем коэффициент нагрузки для проверки контактных напряжений:

;                        (3.23)

При ψ_bd = 1,1 и несимметричном расположении колеса k_нβ = 1,13 [3.стр.39].

k_нα - коэффициент. учитывающий неравномерность распределения нагрузки между зубьями; при V=0,49 м/с и 8-й степени точности k_нα = 1,06 [3.стр.39].

k_нv – коэффициент динамичности; при V = 0,49 м/с и 8-й степени точности     k_нv = 1,0 [3.стр.40].

k_H = 1,13 · 1,06 · 1,0 = 1,2

Проверка контактных напряжений:

;                        (3.25)

.

Условие прочности по контактным напряжениям выполнено.

Силы, действующие в зацеплении:

Окружная:

Н.                      (3.26)

Радиальная:

Н                    (3.27)

Осевая:

Н                     (3.28)

Проверка зубьев на выносливость по напряжениясм изгиба:

                        (3.29)

где: k_p – коэффициент нагрузки:

K_F = K_Fβ · K_FV ;

При ψ_bd = 1,1 и несимметричном расположении колеса K_Fβ = 1,265 [3.стр.43].

K_FV – коэффициент динамичности. При V = 0,49 м/с и 8-й степени точности K_FV =1,1 [3.стр.43].

K_F = 1,1 · 1,265 = 1,4;

Y_F – коэффициент формы зуба:

Для шестерни:

               (3.30)

Для колеса:

               (3.31)

Находим отношения:

                                 (3.32)

                                 (3.33)

Дальнейший расчет ведем для зубьев колеса, так как для него найденное отношение меньше.

Коэффициент Y_β учитывающий поывшение прочности косых зубьев по сравнению с прямыми:

                          (3.34)

Коэффициент К_fα учитывающий неравномерность распределения нагрузки между зубьями:

                               (3.35)

где: Е_α – 1.5 коэффициент торцевого перекрытия [3.стр.47].

n = 8 – степень точности передачи.

;

.

Условие прочности по напряжениям изгиба выполнено.

Проверка зубьев колеса на статическую прочность по кратковременно