






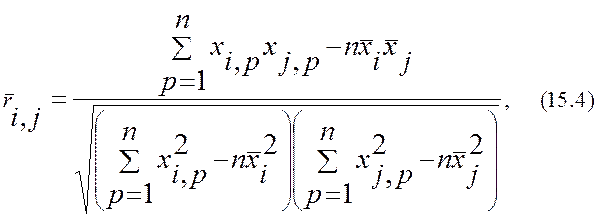
где 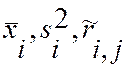 - оценки М(Xi), D(Xi) и парного коэффициента корреляции ri,j соответственно. Оценки парных коэффициентов
корреляции образуют симметричную матрицу
- оценки М(Xi), D(Xi) и парного коэффициента корреляции ri,j соответственно. Оценки парных коэффициентов
корреляции образуют симметричную матрицу ![]() ,
главная диагональ которой состоит из единиц.
,
главная диагональ которой состоит из единиц.
Оценки частных и множественных коэффициентов определяются по формулам, аналогичным формулам (13.12) и (13.16), т.е.
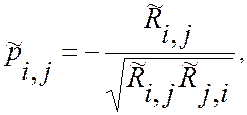
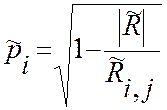
,
где 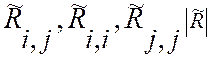 -
алгебраические дополнения и определитель матрицы оценок парных коэффициентов
корреляции.
-
алгебраические дополнения и определитель матрицы оценок парных коэффициентов
корреляции.
16. Критерии значимости коэффициентов корреляции
Пусть по выборке объема n
найдена оценка коэффициента корреляции rB (или
оценки парных коэффициентов корреляции ![]() ).
Проверяется нулевая гипотеза H0: r=0 (или ri,j=0). По уровню значимости
).
Проверяется нулевая гипотеза H0: r=0 (или ri,j=0). По уровню значимости ![]() и числу степеней
свободы v=n-2 по таблицам распределения Стьюдента находим
критическое значение
и числу степеней
свободы v=n-2 по таблицам распределения Стьюдента находим
критическое значение ![]() . Если выполняется
неравенство
. Если выполняется
неравенство
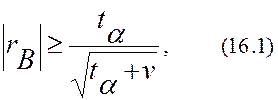
то гипотеза ![]() отвергается,
т.е. коэффициент корреляции не равен нулю. В этом случае говорят, что
коэффициент корреляции значим при уровне значимости
отвергается,
т.е. коэффициент корреляции не равен нулю. В этом случае говорят, что
коэффициент корреляции значим при уровне значимости ![]() .
Если же неравенство (16.1) не выполняется, то нет оснований отвергнуть гипотезу
.
Если же неравенство (16.1) не выполняется, то нет оснований отвергнуть гипотезу
![]() , т.е. коэффициент корреляции
незначим при уровне значимости
, т.е. коэффициент корреляции
незначим при уровне значимости ![]() .
.
Пример 6 (продолжение). Проверить значимость коэффициента корреляции.
Выберем уровень значимости ![]() =0,05 и найдем число степеней
свободы v=10-2=8. Тогда по таблицам
=0,05 и найдем число степеней
свободы v=10-2=8. Тогда по таблицам ![]() =2,3. Критерий значимости
=2,3. Критерий значимости
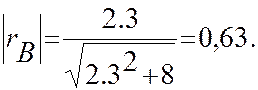
Так как 0,33<0,63, то коэффициент корреляции незначим, т.е. нет оснований считать его отличным от нуля.
Аналогичный критерий значимости
используется и для частных коэффициентов корреляции, но при этом число степеней
свободы v=n-k, где n- объем выборки, k-
число случайных величин в системе. По уровню значимости ![]() и
числу степеней свободы v по таблицам распределения Стьюдента находим
критическое значение
и
числу степеней свободы v по таблицам распределения Стьюдента находим
критическое значение ![]() и далее используем
формулу (16.1), но уже для оценки частного коэффициента корреляции
и далее используем
формулу (16.1), но уже для оценки частного коэффициента корреляции ![]() .
.
Для проверки значимости множественного коэффициента корреляции (в частности коэффициента корреляции для системы двух величин, так как этот коэффициент корреляции является и парным, и «множественным» одновременно) определяется среднее квадратическое отклонение его оценки
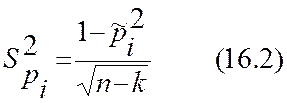 ,
,
где n-объем выборки,
k- число случайных величин в системе.
По числу степеней свободы v=n-k
и уровню значимости ![]() по таблицам распределения
Стьюдента находим
по таблицам распределения
Стьюдента находим ![]() . Критерий значимости
определяется неравенством
. Критерий значимости
определяется неравенством
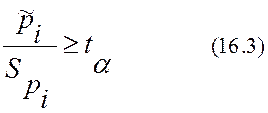 .
.
Отметим, что если по критерию (16.3) проверяется значимость коэффициента корреляции для системы двух величин, то в числителе следует взять модуль его оценки.
17. Оценки коэффициентов регрессии
Пусть по данным выборки (14.1) для системы двух случайных величин требуется оценить коэффициенты линейного уравнения средней квадратической регрессии y=kx+b. Так как сами коэффициенты определяются как аргументы минимума функции S(k,b), определяемой формулой (10.1), т.е. минимумом M((Y-kX+b)2), то для нахождения оценок коэффициентов k и b следует минимизировать оценку этого математического ожидания, т.е. среднее значение. Но так как знаменатель среднего арифметического является постоянным, то достаточно минимизировать числитель, т.е. выражение
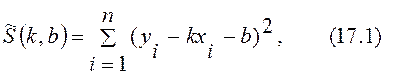
где n-объем
выборки, (![]() )- i-й
элемент выборки (i=1,…..,n).
)- i-й
элемент выборки (i=1,…..,n).
Преобразуем сумму (17.1), при этом для краткости записи не будем указывать пределов суммирования
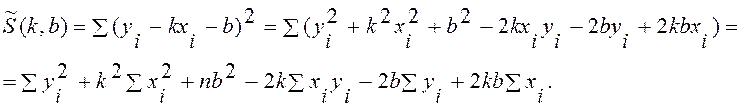
Чтобы найти минимум (17.1), найдем частные производные
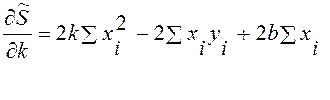
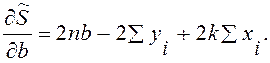
и, приравняв их нулю, сократив на 2 и перенеся известные в правую часть, получим так называемую систему нормальных уравнений метода наименьших квадратов
![]()
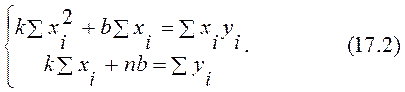
Решив систему (17.2), найдем оценки
коэффициентов регрессии ![]() и
и ![]() .
.
Приведем здесь правило получения системы
нормальных уравнений. При этом мы рассматриваем только такие уравнения,
коэффициенты к которые входят линейно. Как быть в случае, если это не так,
будет рассмотрено позже. Введем матрицу, столбцы которой определяются видом
уравнения регрессии: столбец состоит из трех значений элементов выборки, на
которые умножается коэффициент регрессии с этим номером. При этом свободный
член умножается на 1. Число строк матрицы равно объему выборки. Так, для
уравнения y=kx + b первый коэффициент умножается на x,
следовательно, в первом столбце стоят значения ![]() ,
а второй коэффициент как бы умножается на 1, т.е. второй столбец матрицы
состоит из единиц. Так как коэффициентов в этом примере два, то и столбцов в
матрице только два. Т.е. матрица имеет вид
,
а второй коэффициент как бы умножается на 1, т.е. второй столбец матрицы
состоит из единиц. Так как коэффициентов в этом примере два, то и столбцов в
матрице только два. Т.е. матрица имеет вид
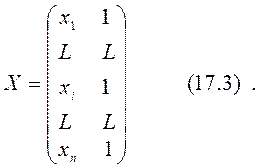
Транспонируем эту матрицу и рассмотрим произведение

которое является матрицей системы нормальных уравнений МНК. Если ввести обозначения
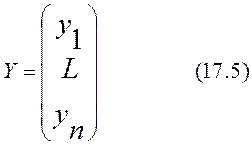 и
и
то система нормальных уравнений (17.2) в матричной форме имеет вид
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.