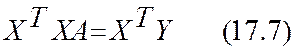Оценки частных и множественных коэффициентов. Критерии значимости коэффициентов корреляции, страница 2

                                                             .                                                            

         Как уже указывалось выше, такая запись справедлива для любого уравнения регрессии, лишь бы только коэффициенты в уравнение входили линейно. Например, для уравнения 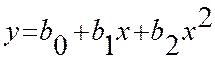 матрицы (17.4) и (17.6) будут иметь вид

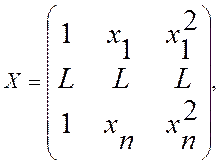
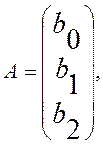
и Y равен  (17.5), и тогда система (17.7) позволит найти оценки коэффициентов  Указанное правило составления системы нормальных уравнений справедливо и для уравнений множественной регрессии. Например, для уравнения  матрицы (17.4)-(17.6) будут иметь вид

    

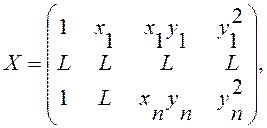
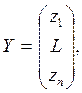
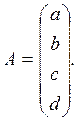
        Отметим, что МНК может быть использован и для аппроксимации функции, заданной таблично, т.е. для случая, когда аргументы и функция не являются значениями каких-либо случайных величин. В некоторых случаях, например. При обработке результатов экспериментов, значения аргументов считаются неслучайными. А функция рассматривается как случайная величина и ошибки  измерений аргументов как бы переносятся на значения функции. Об этом мы будем говорить несколько более подробно ниже.

        Пример 7. Рассмотрим результаты некоторого эксперимента, приведенные в табл.П7. Можно рассматривать X и Y как значения некоторых факторов эксперимента (аргументов), а  Z  как отклик на изменения этих факторов, т.е. функцию. Обратим внимание, что при X=Y=0  Z=0, т.е. можно рассматривать уравнение без свободного члена. Будем искать зависимость в виде

            Тогда

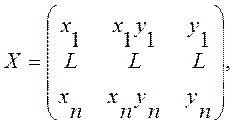
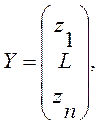
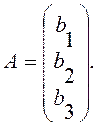
Таблица П7

X	Y	Z
-1	-1	-2.1
0	-1	-2.9
1	-1	-3.1
-1	0	-0.9
0	0	0
1	0	1.0
-1	1	1.1
0	1	3.0
1	1	4.9

     Найдя  и , получим систему нормальных уравнений МНК

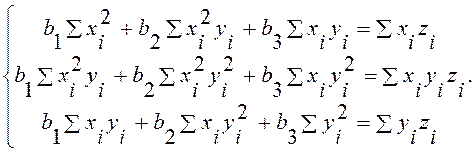
     Упражнение 4. Доказать, что система нормальных уравнений для примера 7 имеет указанный вид, составить ее для приведенных в этом примере данных и решить. (Ответ: z=0,783x+1,200xy+2,850y).

     Как было сказано выше, иногда, в случае когда коэффициенты входят в уравнение нелинейно, путем преобразований удается линеаризовать коэффициенты. Например, для степенной функции

                                                                                                                                  

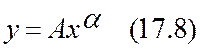
таким преобразованием является логарифмирование

                                                               ,                                                  

и замена Y=lny, X=lnx, k=, b=lnA приводит к линейному уравнению Y=kx+b, для которого справедлива система нормальных уравнений (17.2).

                Для показательной функции

                                                                                                                                 

преобразованием, приводящим к линейному уравнению, также является логарифмирование

                                                                                                                      

с заменой Y=lny, k=, b=lnA  и системой нормальных уравнений (16.2). Другие примеры функций и преобразований можно найти, например, в И.Н. Бронштейна, К.А. Семендяев. (Справочник по математике. –М.: - 1954.- С.578-584.

           Пример 8. Найти коэффициенты степенной функции (17.8) по данным, приведенным в первых двух столбцах табл.П8.

Таблица П8

x	y	X=lnx	Y=lny		XY
0	0	-----	-----	-----	----
0.5	0.51	-0.693	-0.673	0.480	0.466
1	2.95	0	0.668	0	0
1.5	4.52	0.405	1.509	0.164	0.611
2	7.97	0.693	2.076	0.480	1.439
2.5	16.45	0.916	2.800	0.839	2.565
	Cумма	1.321	6.380	1.963	5.081

        В соответствии с (17.2) система нормальных уравнений и

1,963k + 1,321b = 5,081

 1,321k + 5b = 6,380

Отметим, что первая строка не участвует в составление системы, поэтому n = 5. Решая систему, находим k = 2,104 и b = 0,72019. Тогда a = k = 2,104 и A = e^b = e^0,72019 = 2,054 и искомое уравнение средней квадратической регрессии y = 2,054x^2,104. Следует учесть, что в этом случае найденные коэффициенты регрессии обеспечивают не минимум суммы квадратов отклонений расчетных значений от фактических, а минимум суммы квадратов отклонений логарифмов расчетных значений от логарифмов фактических значений т.е.

.

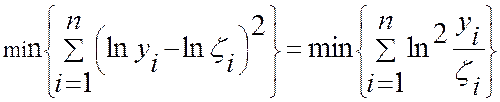18. Значимость коэффициентов регрессии

Пусть нужно найти оценки коэффициентов средней квадратической регрессии y = f(x₁,…, x_k, a₁,…, a_l ). По виду этого уравнения по данным выборки составлены матрицы X, Y и A. После решения системы нормальных уравнений получена зависимость