Транспортная задача по определению числа ящиков, которое нужно перевести с каждого завода на каждый склад для минимизации транспортных расчетов

Транспортная задача

Пусть имеется два завода   : первый   и   второй

                     и три склада   : А, В и С.

 Наличие ящиков с продукцией на заводах и потребности на складах приведено в табл.1.

Таблица 1

Наличие	Потребности
Первый завод   “1”  — имеет  350 ящиков	склад   “А”   —   300 ящиков
	склад   “В”   —   300 ящиков
Второй завод    “2”  — имеет  650 ящиков	склад   “С”   —   300 ящиков
Итого   1000 ящиков	Итого   900 ящиков

Излишки производства (100 ящиков) должны оставаться на месте.

          Стоимости перевозки в денежных единицах (ДЕ) каждого ящика от любого завода до любого склада приведены в таблице 2.

Таблица 2

Заводы	Склады
	“А”	“В”	“С”
Первый  -  “1”	2,5	1,7	1,8
Второй   -  “2”	2,5	1,8	1,4

Задача состоит в том, чтобы определить число ящиков, которое нужно перевести с каждого завода на каждый склад для минимизации транспортных расчетов.

Построение модели начнем с технологического процесса, состоящего в перевозке с первого завода на первый склад.

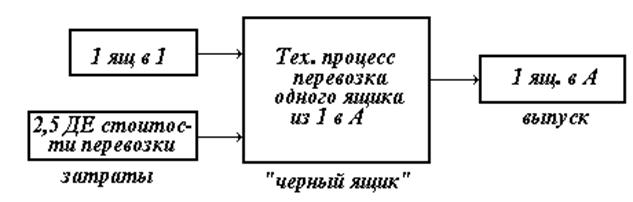
Схема 1.  Схема транспортного технологического процесса

Перевозка ящиков с первого завода на склад А показана на схеме 1. В качестве затрат она требует двух ингредиентов: одного ящика на заводе 1 и 2,5 ДЕ расходов.

В качестве выпуска она производит один ингредиент: один ящик на складе А. Основное предположение состоит в том, что Х ящиков, которые должны быть отправлены из 1 в А потребуют в качестве затрат 1Х ящиков и 2,5Х - расходов. В качестве выпуска 1Х ящиков на складе А.

В рассматриваемом случае выпуск есть аналогичный ингредиент, но в другом месте. Можно также хранить продукцию на заводах, что приводит к технологическому процессу, состоящему в хранении.

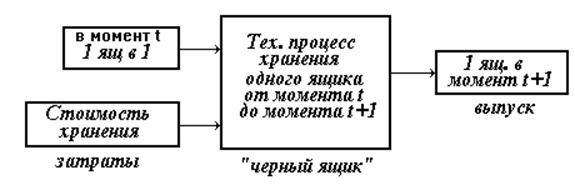
Схема 2.

Сходство технологических процессов описанных на схемах 1 и 2 состоит в том, что перевозка есть преобразования в пространстве, а хранение  —  преобразование во времени.

В виду того, что в нашей конкретной задаче мы не будем рассматривать ни выпуск в более поздние моменты времени (хранение), ни приписывая стоимость хранению процессы хранения на заводах 1 и 2 примут вид:

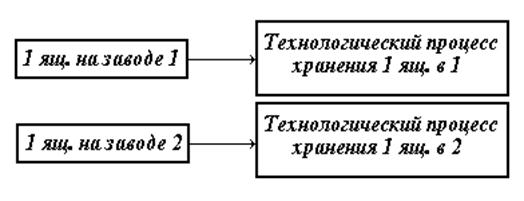
Схема 3.

Шаг 1. Начнем с составления списка восьми возможных процессов перевозки и хранения. В качестве единицы измерения перевозки или хранения выберем 1 ящик.

Перечень технологических процессов

1.  Перевозка от 1 до А

2.  Перевозка от 1 до В

3.  Перевозка от 1 до С

4.  Перевозка от 2 до А

5.  Перевозка от 2 до В

6.  Перевозка от 2 до С

7.  Хранение излишков в 1

8.  Хранение излишков в 2

Шаг 2. Можно было бы полагать, что кроме стоимостей имеется еще только один вид ингредиента (ящик), но экономисты указывают, что аналогичный ингредиент в разных местах или в разные моменты времени является в сущности различными ингредиентами. В этой задаче мы игнорируем изменение во времени и сосредоточимся только на перемещениях из одних мест в другие. Согласно этому получится список из 6 ингредиентов, отражающих два завода, три склада и ингредиенты стоимости (деньги).

Перечень ингредиентов

1.  Ящик в 1

2.  Ящик в 2

3.  Ящик в А

4.  Ящик в В

5.  Ящик в С

6.  Стоимость перевозки в ДЕ

Шаг 3. При выписывании коэффициентов затрат– выпуска в модели будет использоваться следующее соглашение о знаке коэффициента. Затраты будут считаться положительными, а выпуск  —  отрицательными.

Коэффициент затрат выпуска для каждого технологического процесса представим в виде таблицы 3.

Таблица 3

Ингредиенты	Технологические процессы
	1	2	3	4	5	6	7	8
1. Ящики в 1	+1	+1	+1				+1
2. Ящики в 2				+1	+1	+1		+1
3. Ящики в А	-1			-1
4. Ящики в В		-1			-1
5. Ящики в С			-1			-1
6. Стоимости в ДЕ	+2,5	+1,7	+1,8	+2,5	+1,8	+1,4

Каждому технологическому процессу в этой таблице соответствует вертикальный столбец, а каждому ингредиенту  —  горизонтальная строка. На их пересечении помещен коэффициент затрат–выпуска со знаком того ингредиента, который требуется единичной интенсивностью технологического процесса. Таким образом, технологический процесс 4, примененый с единичной интенсивностью для перевозки одного ящика из 2 в А имеет в качестве затрат один ящик в 2 (коэффициент затрат выпуска +1 в строке 2 ,столбец 4) и 2,5 ДЕ (коэффициент затрат выпуска +2,5 в строке 6, столбец 4). В качестве выпуска он имеет один ящик в А (коэффициент затрат выпуска -1 в строке 3, столбец 4).

Шаг 4. Экзогенные (внешние) потоки, поступающие в систему и требуемые от системы как целого, показаны на схеме 5. Денежные затраты, как экзогенный поток, пока неопределенны и будут обозначаться через Z. Они должны быть как можно меньше.

Экзогенные потоки

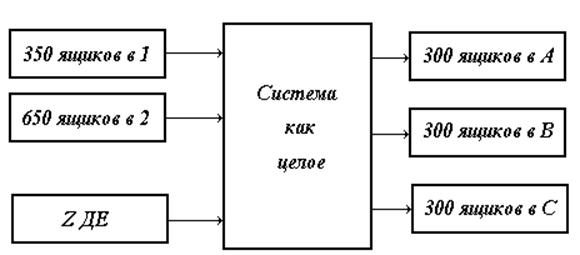
Схема 5.

Полезно выписать эти экзогенные потоки в столбец, упорядоченный по ингредиентам, где должно использоваться тоже самое соглашение о знаках, которое принято относительно потоков в каждый технологический процесс внутри системы. Так как алгебраическая сумма потока по всем технологическим процессам будет приравнена к экзогенным потокам, образуя уравнения материального баланса.

Таблица 4

Шаг 5. Сопоставим каждому из технологических процессов 1,2,...,8 неизвестную и подлежащую определению величину, которая представляет собой интенсивность этого технологического процесса:

Х₁, Х₂,...,Х₈.

Используя табл. 3 легко записать уравнения материального баланса для системы по каждому ингредиенту.

Для ингредиента 1 (ящики в 1) технологические процессы, потребляющие его есть 1,2,3, и 7. Ввиду того, что коэффициенты затрат выпуска связанные с ингредиентом 1 все равны ”+1”, чистый поток этого ингредиента:

Этот поток должен быть равен экзогенному потоку в систему первого ингредиента, который равен 350. В результате первое уравнение материального баланса принимает вид:

Аналогично для второго ингредиента:

Для третьего ингредиента

Для четвертого ингредиента

Для пятого ингредиента

Наконец, поток в системе шестого ингредиента:

Приведем это выражение к виду уравнения материального баланса, приравнивая этот поток к неопределенным денежным затратам Z.

Z надо минимизировать.

Если это объединить в систему, то получим модель в форме уравнений. Модель в табличной форме имеет вид табл. 5

 .
Таблица 5

Ингредиенты	Технологические процессы								Экзогенные
	1 Х1	2 Х2	3 Х3	4 Х4	5 Х5	6 Х6	7 Х7	8 Х8	потоки
Ящики в 1	1	1	1				1		350
Ящики в 2				1	1	1		1	650
Ящики в А	-1			-1					-300
Ящики в В		-1			-1				-300
Ящики в С			-1			-1			-300
Стоимости, ДЕ	2,5	1,7	1,8	2,5	1,8	1,4			Z (min)

Задача состоит в том, чтобы определить интенсивности технологического процесса Х₁, _Х2,...,Х₈, которые:

—  неотрицательны ;

—  удовлетворяют уравнениям материального баланса;

—  минимизируют величину Z - Z (min).