Обобщенные координаты. Функция Лагранжа. Принцип наименьшего действия. Законы сохранения импульса, момента импульса и энергии

Очевидно, что из принципа наименьшего действия функция Лагранжа определяется с точностью до аддитивной функции d F q t_t ( , ), т.к. уравнения Лагранжа для функций L₁ и L₂ (q q t, , ):= L q q t₁ ( , , )+ d F q t_t ( , ) совпадают.

2. Законы сохранения импульса, момента импульса и энергии. Их связь с однородностью и изотропностью пространства и однородностью времени.

Интеграл движения – функция координат и скоростей, остающаяся постоянной при движении системы и зависящая только от начальных условий. ([1] с. 24)

Число интегралов движения для системы с N степенями свободы – 2N −1

Аддитивный интеграл движения – интеграл движения, значение которого для системы равно сумме его значений для невзаимодействующих (?) подсистем, составляющих данную систему.

L ≠ L t( )

Однородность времени.  (требование для замкнутой системы)

∇         d L q q_t ( , ) = ∂_qL q + ∂_qL d q_t        = ∂_qL q + d_t ∂_qL q − d_t∂_qL q         ⇒

                                                                                   d_t∂ −∂ =_qL           _qL 0

⎫

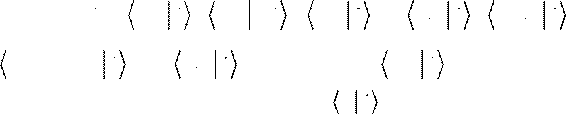d_t∂_qL −∂_qL q = d_t ⎡⎣ ∂_qL q − L⎤⎦ ⇒ ∂_qL q − L = const ⎬⎪ ⇒ p := ∂_qL − обобщённыйимульс E := p q − L − энергия ⎪⎭

E = const

▲  закон сохранения энергии

Однородность пространства. Механические свойства системы не изменяются при любом параллельном переносе системы как целого в пространстве (ДПСК): δL x( ) = 0

∇ 0 =δL x( ) = L x( +δx)− L x( ) = L x( +δx)− L x x( , ) ≈ L x( )+ ∂_xL δx − L x( ) ⇒

                             d_t∂ −∂ =_xL                                                                                             _xL 0    p=∂_xL

        ∂_xL = 0        ⇒       d_t∂_xL = 0    ⇒   ∂_xL = const     ⇒

p = const

▲  закон сохранения импульса

Замечание. Импульс системы равен сумме импульсов частиц её составляющих (вне зависимости от наличия взаимодействия между ними). Проекция импульса сохраняется в том случае, когда потенциальная энергия не зависит от соответствующей декартовой координаты. ([1] с. 27)

δL x x( , ) = 0,

δ δϕxi =  × xi

Изотропия пространства. Механические свойства системы не изменяются при повороте системы как целого 

                                  ...                                                         d_t∂ −∂ =_xL                                                                   _xL 0  p:=∂_xL

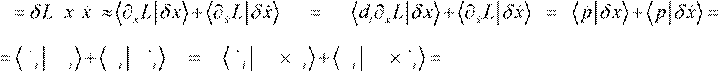∇ 0 =δL x x( , )≈ ∂_xL δx + ∂_xL δx          =        _{t    x}

δ δϕxi = ×xi

            = p_i δx_i + p_i δx_i               =      p_i δϕ× x_i + p_i δϕ× x

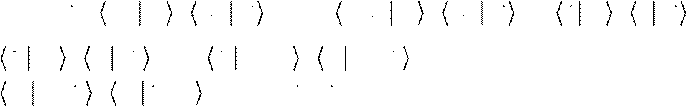          = δϕ x_i × p_i + δϕ x_i × p_i           ⇒   x_i × p_i + x_i × p_i = 0   ⇒   d_t [x_i × p_i ] = 0   ⎫⎪

⎬ ⇒

         M := x_i × p_i − моментимпульсасистемы                                                    ⎪⎭

M = const

▲  закон сохранения момента импульса

Замечание. Момент импульса – аддитивный интеграл движения (вне зависимости от наличия взаимодействия между частицами).

Утв. Любая замкнутая система всегда имеет семь аддитивных интегралов движения:

E , p , M . ([1] с. 32)

3. Движение в центральном поле. Интегралы движения. Уравнение траектории.

Локальные обозначения: r – радиус-вектор, x, ,y z – координаты частицы в ДПСК, модули векторов – курсив, вектора – жирный курсив,

Утв. При движении в центральном поле выполняется закон сохранения момента импульса:

         M = const    ⎫

⎬ ⇒ движение происходит в плоскости, уравнение которой M r = 0

         M = r× p    ⎭

Введём ПСК в плоскости движения M r = 0

            x = rcos ,ϕ y = rsinϕ ⇒       x = r cosϕ ϕ ϕ−r sin                  , y = rsinϕ ϕ ϕ+ r                           cos                                      ⎫ ...

⎪ m   ^⎬⇒ L =T −U ⁼          (x² + y² )−U _⎪

                                  2                                                                                                     ⎭

                                                                                             m    ^{2          2    2}

L  r r( , ,ϕ) =     (r + r ϕ )−U r( )

2

В данном случае ϕ – циклическая координата, т.к. функция Лагранжа не зависит от неё явным образом.

        Утв. q_i – циклическая       ⇒     p_i – интеграл движения

∇ очевидно из уравнения Лагранжа и определения обобщённого импульса ▲

Уравнение Лагранжа для ϕ примет вид:
▲  2                  ⎫ dt∂ϕL = 0      ⇒       pϕ = mr ϕ= const           ⎪ ⎬ ⇒	M = const , т.е. M – интеграл движения

...

M  = rp = mx² + y² )(x² + y² ) =mr²ϕ ⎪

⎭

Т.к. функция Лагранжа явно не зависит от времени, то E – интеграл движения.

Нахождение r и уравнения траектории с помощью интегралов движения E и M ([1] с. 47)

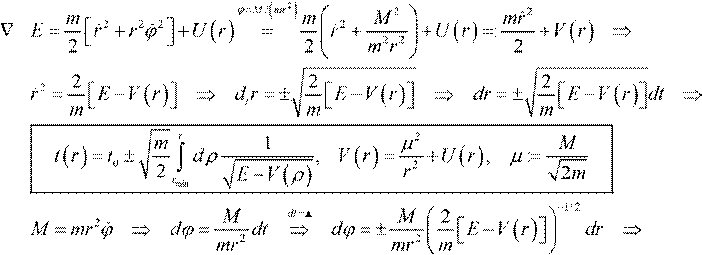mr

r 1 ϕ ϕ μ ρ( )r =          0 ± ∫ d 2 rmin ρ E −V ( )ρ

▲  уравнение траектории

Замечание. В уравнении траектории знак ± означает, что имеются две ветви траектории, расположенные симметрично относительно прямой, проходящей через начало координат под углом ϕ₀ , что имеет место в случае инфинитного движения (и только?).

В зависимости от вида потенциала U возможны два типа движения:

∀t     r t( )∈[r_min ,∞) – инфинитное движение     ∀t      r t( )∈[r_min ,r_max ] – финитное движение

Область значений r является решением неравенства: E −V r( ) ≥ 0

Точки поворота – корни уравнения E −V r( ) = 0 . Очевидно, что точках поворота r = 0.

Таким образом, движение в центральном поле полностью определяется видом потенциала U и значениями параметров E и M .

4. Рассеяние частиц неподвижным силовым центром. Дифференциальное сечение рассеяния. Формула Резерфорда.

Рассмотрим случай инфинитного движения, т.е. имеется единственная точка поворота r_min . Частица с энергией E налетает на рассеивающий центр из бесконечно удалённой точки.

Уравнение траектории:

r        1          μ²             M ϕ ϕ μ ρ( )r =      ₀ ^±      r_min∫ d     2                  ,           E −V r( _min ) = 0,        V r( ) ⁼ r₂ +U r( ), μ:=     2m ρ E −V ( )ρ

⎫

                                 t⎪ ▲                                                           +∞                            1               ▲

                                                                                ⎬⇒ ϕ = μ ρ∫ d⇒ ϕ(r                     ) =ϕ

        t → −∞  ⇒2     r → +∞   ⎪⎭        ₀                  r_min ρ2          E −V ( )ρ              _{min              0}

Пояснения.

1.  Выбор СК.

2.  Частица налетает из бесконечно удалённой точки θ:=π ϕ−2 ₀ – угол рассеяния

От параметров E и M перейдём к новым параметрам задачи.

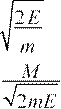E =                             ⇒ υ_∞ =    – скорость частицы на бесконечности

▲

        M =:bmυ_∞       ⇒         b = – прицельное расстояние

Выражение для угла рассеяния примет вид:

                                          +∞                                  1                          b2        U r( ^min )

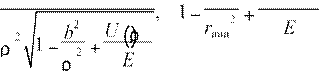θ(b E, ):=π− 2b ∫ dρ= 0

rmin

Сопоставление с экспериментом.

 поток невзаимодействующий между собой частиц, налетающих на рассеивающий силовой центр. Исходя из симметрии задачи, перейдём в ЦСК. dσ π= 2 bdb = 2π θb∂_θbd ⎫ dΩ

                                                                 ⎬ ⇒  dσ π= 2 b∂^θb    ⇒

        dΩ = 2π θθsin d                 _⎭                          2π θsin

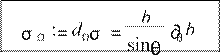 дифференциальное сечение рассеяния

Дифференциальное сечение определяет приращение телесного угла рассеяния, соответствующего приращению площади кольца.

dN = n2πbdb =:ndσ ⇒ dN = nσ_ΩdΩ – физический смысл дифференциального сечения рассеяния.

dN – число налетающих частиц, проходящих через кольцо 2πbdb, а также число рассеянных частицы в соответствующий телесный угол dΩ, в единицу времени n – плотность потока налетающих частиц

 интегральное сечение рассеяния

Замечания.

1.  В эксперименте регистрируется число частиц dN , рассеянных в телесный