Двоичное растяжение, двухпараметрический сдвиг. Преобразование Габора и частотно-временные окна

1  Базовый конспект по вэйвлетам

1.1 Вейвлеты

Пусть 7, : К         ... — множество целых чисел, и vb(x) Е L1 (—ос, ос) некоторая функция.

Рассмотрим функции, порожденные сдвигом (х) = gb(x — К) = Е Е — оператор сдвига. Рассмотрим также растяжения

= ерЈх - К), j,k e Z Двоичное растяжение, двухпараметрический сдвиг. Введем нормировку

(1)

                                                            (2)

Тогда функции

, j,k e Z

назовем нормированными вейвлетами. Функцию vb(x) назовем базисным вейвлетом. Пусть выполняется

ЛК(3)

Тогда получаем ортогональную систему вейвлетов. Функцию ] (х) ос) можно разложить в ряд по ортогональной системе вейвлетов

                                                  (4)

т.е. функции f(x) отвечает набор чисел на целочисленной двумерной сетке Аналог ряда Фурье и коэффициентов Фурье. Коэффициенты вейвлет-разложения находятся как сјк =< f,ejk >=                             (5)

Здесь рассматривается вещественный случай

Помимо ортогональной системы можно рассмотреть полуортогональную систему

 = О при ј                                                    (6)

1.2 Преобразование Габора и частотно-временные окна

Рассмотрим преобразование Фурье

                                          (7)

где f(x) е Ь (—ос, ос). Оно плохо тем, что глобально. Постараемся ввести выделяющее окрестность на оси t с помощью функции Ка (t) = (206)— е — гауссиана. Множитель выбран так, чтобы выполнялась нормировка“

                                                              (8)

Вычислим также обычную норму

1/2

К 12 =         ka² (t)dt                                        (9)

1

Оба результата следуют из вычисления классического интеграла

                                                        (10)

Введем ”полуширину" функции
llt2ka112               t2 (t)dt            /llka112 Рассмотрим преобразование Фурье от функции Габора	(11)
k1/4a(w) =            eiwt ka (t)dt, Введем обратное преобразование Фурье	(12)
ЛО = Можно показать, что	(13)
k114a(W) е   Можно показать, что функция k1/4a(w) характеризуется на оси полушириной	(14)
1 26 С полуширинами свяжем частотно-временное окно.	(15)

(16)

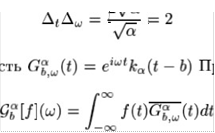Введем преобразование Габора. Пусть           (t — Ь) Преобразование Габора определяется

(17)

Оно вырезает частотно-временное окно в преобразовании Фурье. Имеем также

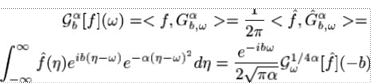                                (18)

Можно отказаться от преобразования Фурье и частотно-временное оконное преобразование.

1. З В-сплайны

С точки зрения общей теории сплайнов В-сплайны — это сплайны дефекта 1 с минимальным носителем. Будем строить их рекурсивным образом. Определим

N1(x) = диее	(19)
ЛТ2(г) = М(г) * М(г) =t)dt =	(20) х е [1,2)

2

Далее по индукции

Nm(x) = * N1(x) =                  (21)

Итак В-сплайн Мп (х) на интервале [К, К + 1], К т задан полиномом К — 1 порядка, является сплайном дефекта 1, и носитель его интервал [О, т). Кроме того справедливо

Nm(x) > О, х

N(m/2 + х) = N(m/2 - х)

 Справедлива формула дифференцирования

N'm(x) = Мп -1 (х) -                   - 1) Удобнее всего строить В-сплайны из рекуррентных соотношений Докажем это по индукции, проинтегрировав предыдущее равенство

(22) (23)

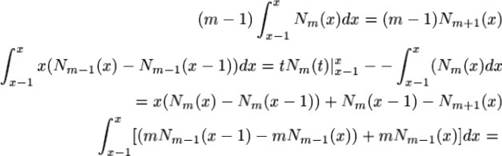
—mNm(x) +           — 1) — mNm(x)			(24)
Собирая все вместе, найдем
mNT+1 (х) =         (х) — Nm(x — 1)) + (т + Вычислим преобразование Фурье АЛ (t)		— 1)	(25)
1                            е 'wt dt = е—iwt10 = (1 По теореме о преобразовании Фурье свертки	е		(26)
iwm 1.4 Сплайн-вэйвлеты			(27)
Введем сплайн-вейвлеты т-го порядка по В-сплайнам т-го порядка

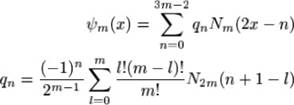                                          (28)

Носитель -интервал [О, 2m — 1). Доказательство, что именно такой выбор коэффициентов приводит к ортогональности по т.е. к полуортогональным вэйвлетам, достаточно трудно, и не приводится.

з

Полуортогональный вэйвлет-базис можно трансформировать в биортогональный вэйвлет-базис, введя двойственные вэйвлеты. Пусть

                                                 (29)

По ф(”) восстанавливаем р(х). Функция р(х) называется двойственным к вэйвлетом. Выполняется свойство ортогональности (без доказательства)

 ejk'         5jl6km

1.5 Интегральное вэйвлет-преобразование

Введем интегральное вэйвлет преобразование

                                 (30)

Это аналог преобразования Фурье и преобразования Габора, т.е. краткомасштабное оконное преобразование

Если f(x) = ЕСјКфјк(х), сјк =< f,ejk >

Cjk =

Есть несколько формул восстановления. Для нас важно связать с двойственным вэйвлетом. В этом случае имеем формулу восстановления

 < f'Vjk > рјк(х) =              Л рјк          (х)                (31)

4