Обратное воздействие среды на волну. Дифференциальные уравнения для амплитуды поля или укороченные волновые уравнения

Обратное воздействие среды на волну. Дифференциальные уравнения для амплитуды поля или укороченные волновые уравнения.

Излучение диполей среды изменяет проходящую мимо световую волну. Это изменение проявляется в поглощении света и изменении скорости распространения света в среде. Изменения в проходящей световой волне возникают в результате интерференции света переизлученного диполями молекул и проходящей мимо световой волны. В этом и состоит обратное воздействие среды на волну.

Вместо сложения волн излучения диполей изменение световой волны в среде можно вывести из системы уравнений Максвелла. Что мы и сделаем.  Рассмотрим систему уравнений Максвелла

div D( ) = 4πρ 

                    ( )    1 ∂B

rot E = −_c ⋅ ∂_t

                                              

div B( ) = 0



           rot H( ) = 4cπ j + 1c ⋅ ∂∂Dt

            без свободных зарядов ρ=0 и без токов проводимости j =0.

          Тогда получим:

div D( ) = 0 

                    ( )    1 ∂B

rot E = −c ⋅ ∂t

                                     .

div B( ) = 0



               rot H( ) = 1 ⋅ ∂D

                           c   ∂t

           Рассмотрим два выражения для ротора ротора E .

С одной стороны, возьмем ротор от второго уравнения и подставим в правую часть вместо ротора B выражение для ротора H из четвертого уравнения. Напомним, что в оптике µ=1 и B H= . Тогда получим

                       (  ( ))   1   ^∂     ( )     1   ^∂2D

 rot rot E = − ⋅ rot B = − ⋅ . c ∂t c2 ∂t2

А с другой стороны по правилу "бац минус цап":  rot rot E( ( )) = _∇,_∇,E__ = ∇ ∇( ,E) − E(∇ ∇, ).

Здесь 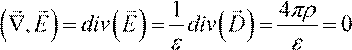, тогда           rot rot E(  ( )) = −E(∇ ∇ = −∆, )     E .

           Объединяя оба выражения для rot rot E( ( )), получим:

1  ∂2           ∆E −     ⋅    D = 0  2  ∂t2 c ---------	(4.1)
Если подставить уравнение для поля E:	D =εE в уравнение (4.1), то получим волновое
ε ∂2           ∆E −     ⋅ E = 0	(4.2)

                             c2    ∂_t2

Сравнивая уравнение (4.2) с определением волнового уравнения в математике:

                               1    ∂²E

          ∆E −      ⋅        = 0,

                            V 2    ∂_t2

  получим величину фазовой скорости световых волн V ^{= c} . Сравнивая

ε

величину скорости с определением показателя преломления V = ^c , получаем n

             n = ε, точнее n = εµ, но в оптике µ≈1.

          Тогда ε= n²                   =>      D = n E²

---------

Векторы D и E можно связать друг с другом и несколько иначе:  D = E + 4πP, где P — поляризация среды или объемная плотность дипольного момента, осциллирующая на световой частоте.

         Разобьем поляризацию на два слагаемых P = P_нерез + P_рез :

         D = E + 4πPнерез + 4πPрез.

Здесь P_рез — резонансный вклад в поляризацию или вклад двух уровней энергии, связанных переходом близким по частоте к частоте света; P_нерез — нерезонансный вклад в поляризацию среды от остальных переходов.

По аналогии с формулой D = ^{n E2} запишем E + 4πP_нерез = n E₀² , где n₀ — показатель преломления среды вдали от рассматриваемой линии поглощения.

Тогда

         D = n E₀² + 4πP_рез.

Чтобы не тянуть за собой во всех формулах нижний индекс у поляризации будем во всех последующих формулах вместо P_рез писать просто

P, подразумевая под P вклад в поляризацию только от рассматриваемого перехода среды.

---------

Подставим D = n E₀² + 4πP_рез в уравнение (4.1), заменим P_рез на P и получим

                                                                     (4.3)

                               c2 ∂t2          c2 ∂t2

Это  — уравнение Даламбера или волновое уравнение с источниками поля.

Далее из этого уравнения мы хотим получить дифференциальное уравнение для амплитуды светового поля через амплитуду поляризации. Эти уравнения для амплитуд и называются укороченными волновыми уравнениями.  Будем рассматривать уравнение (4.3) для комплексных E и P. Для линейного уравнения с вещественными коэффициентами вещественная часть комплексного решения является вещественным решением.

Рассмотрим световую волну, распространяющуюся вдоль оси z, и линейно поляризованную вдоль оси y . Тогда P E e|| || _y . Для краткости записи отбросим векторные обозначения, и будем рассматривать только y проекции векторов.

Чтобы отличать комплексные величины от вещественных величин будем писать волну над комплексными величинами.  E = Re(E^ɶ) и P = Re(P^ɶ).

          Перепишем уравнение (4.3) для комплексных величин:

                                            Eɶ            Pɶ

          ∆E −     ⋅        =      ⋅                                                                 (4.4)

                               c2 ∂t2          c2 ∂t2

          Будем искать решение в виде

          E^ɶ = E^ɶ₀(t z, )⋅e^iϕ,          где     ось     z         направлена вдоль направления распространения световой волны ϕ ω=   t − k z₀ +^ϕ₀ — фаза световой волны и будем рассматривать фазу, как фазу волны распространяющейся с фазовой c     c

скоростью   , а не со скоростью     , как на самом деле. Соответственно n₀          n

k₀ ⁼ λ λν^2π₀ = ^2πν₀ = ^ω_c = ⁿ⁰_c^ω — нерезонансное волновое число вместо k = ⁿ_c^ω.

n0

Несоответствие k₀ настоящему k спрятано в зависимости амплитуды света E^ɶ₀ от z координаты.

          Аналогично будем считать

        P^ɶ = P t z^ɶ₀( _, )⋅e^iϕ, где ϕ ω= t − k z₀ +^ϕ₀.

    Получим теперь из уравнения (4.4) связь комплексных амплитуд E^ɶ₀ и P^ɶ₀.

В уравнение надо подставить вторые производные, для которых введем более компактные обозначения:

            ∂2Eɶ Eɶ ''

 ≡

∂ z²

 2 ɶ

  ∂∂tE2 ≡ Eɺɺɶ



              ∂2Pɶ  ɺɺɶ

                ≡ _P

 ∂t2

Выразим эти производные через амплитуды поля и поляризации и подставим в уравнение (4.4).

          Дифференцируя      по       z       выражение     E^ɶ = E^ɶ₀ (t z, )⋅e^iϕ,                 получим

Eɶ ' = E eɶ0' iϕ−ik E e0 ɶ0 iϕ. Тогда

  Eɶ '' = E eɶ0'' iϕ− 2ik E e0 ɶ0' iϕ− k E e02 ɶ0 iϕ.

          Аналогично:

  Eɺɺɶ = E eɺɺɶ0 iϕ+ 2i E eωɶɺ0 iϕ−ω2E eɶ0 iϕ

          и

  Pɺɺɶ = P eɺɺɶ0 iϕ+ 2i P eωɺɶ0 iϕ−ω2P eɶ0 iϕ.

    Подставим все три выражения в уравнение (4.4), в котором  , так как световая волна распространяется вдоль оси z, поэтому нет зависимости от координат x и y и вторые производные по ним равны нулю. После подстановки производных в уравнение (4.4) сократим это уравнение на e^iϕ и получим:

Eɶ0'' − 2ik E0 ɶ0' − k E02 ɶ0 − n022 Eɺɺɶ0 − n022 2i Eωɶɺ0 + n022 ω2Eɶ0 = 4π2 Pɺɺɶ0 + 8πω2i         Pɶɺ0 − 4π2 ω2Pɶ0 c  c        c        c        c        c

                                                                                                                (4.5)

^{2 ɶ} и ^{+ n0}2 ω²E^ɶ₀ в сумме равны нулю, так как k₀ ^{= n0}ω.

          Слагаемые −k E_{0 0}          c_{2                                                                              c}

          Сократим эти два слагаемых в уравнении (4.5).

Амплитуды E^ɶ₀ и P^ɶ₀ — медленные функции координат и времени. Тогда высокими производными от амплитуд можно пренебречь по сравнению с низкими производными. Оставим в уравнении (4.5) только наибольшие слагаемые P^ɶ₀ , E^ɺɶ₀, E^ɶ₀^' для амплитуд