Определение радиуса кривизны поверхности линзы методом колец Ньютона. Кольца Ньютона. Уточнение модели экспериментального материала

Лабораторная работа №122

Определение радиуса кривизны поверхности линзы методом колец Ньютона.

Цель работы. Цель работы – определить радиус кривизны выпуклой сферической поверхности (одной из поверхностей стеклянной линзы) методом колец Ньютона.

Метод колец Ньютона является распространенным и простейшим средством оценки радиусов кривизны оптических поверхностей в лабораторной практике. При этом более точные методы и устройства в большинстве своем основаны на тех же самых идеях, что и рассматриваемый метод.

 Кольца Ньютона.

Если на выпуклую поверхность линзы положить плоскопараллельную пластинку, то между линзой и пластинкой окажется тонкий слой воздуха. Если на эту систему падает пучок монохроматического света, то световые волны, отраженные от верхней и нижней границ слоя, будут интерферировать.

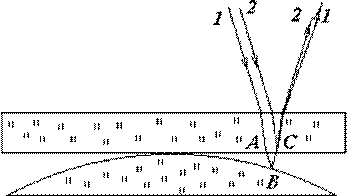
Рис.1

На Рис.1 показаны два интерферирующих луча. Луч 1 проходит воздушную прослойку AB, отражается точке B от поверхности линзы и в точке C интерферирует с лучом 2, который отражается от поверхности пластинки. Результат интерференции зависит от оптической разности хода этих лучей. Если толщина воздушного слоя равна δ , то оптический путь одного из лучей будет длиннее на 2δ ; кроме того, при отражении света от более плотной среды фаза волны меняется на π , что соответствует добавочной разности хода ^λ/2, где λ – длина волны излучения. Следовательно, оптическая разность хода интерферирующих лучей будет

                                                                                        ∆= 2δ +λ/2                           (1)

Так как разность хода зависит от толщины воздушного слоя δ , то в разных точках пластинки мы обнаружим различный результат интерференции: либо увеличение, либо уменьшение амплитуды световых колебаний – будут наблюдаться интерференционные полосы равной толщины. Для всех точек, расположенных на одной окружности с центром в точке соприкосновения плоской поверхности пластинки со сферической поверхностью линзы, толщина воздушного слоя δ одинакова, поэтому интерференционная картина имеет вид чередующихся темных и светлых концентрических колец. Эти кольца и называются кольцами Ньютона.

Светлое кольцо образуется, когда разность хода лучей равна целому числу длин волн:

                                                                                                      ∆ = mλ                           (2)

а темное – полуцелому:

∆ =^m + ^1λ       (3)   2

Здесь m – порядок интерференции – целое число, указывающее, сколько длин волн укладывается в разности хода ∆ . Для центра интерференционной картины δ ⁼ 0, следовательно, ∆=^λ /2 и m ⁼ 0 – т.е., в центре образуется темное пятно. Первая пара светлого и темного колец соответствует m ⁼1, вторая